Когда в задаче B2 фигурируют скидки, но требуется найти общую стоимость товара, будьте особенно внимательны: многие ученики правильно считают проценты, но забывают выполнить второй шаг — собственно, вычислить общую цену.
Сегодня мы рассмотрим простые на первый взгляд задачи, однако многие ученики, сталкиваясь с ними на практике, часто допускают глупые и обидные ошибки. Давайте посмотрим.
Задача B2. Пирожок в кулинарии стоит 18 рублей. При покупке более 20 пирожков продавец делает скидку 10% от всей стоимости покупки. Покупатель купил 30 пирожков. Сколько рублей он заплатил за покупку?
Итак, первый шаг: один пирожок стоит 18 рублей, а наш покупатель вознамерился купить целых 30 пирожков. Давайте пока забьем на скидку и просто посчитаем, сколько бы заплатил наш покупатель за 30 пирожков, если бы каждый из них стоил 18 рублей. Обозначим это число за S. Для того, чтобы его найти, нужно просто 30 умножить на 18:
S = 30 · 18 = 540
Итого, без учета скидки 30 пирожков обошлись бы нам в 540 рублей. А теперь давайте учтем скидку. Для этого воспользуемся стандартной формулой процентов:
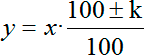
В этой формуле переменная х означает начальное значение, k — проценты, на которые эта величина изменяется и, наконец, y — конечное значение, полученное после изменения величины x на k%. Плюс и или минус перед k ставится в зависимости от того, увеличивается или уменьшается величина х по условию задачи. Очевидно, в нашем случае будет стоять минус, потому что скидка означает уменьшение стоимости.
Если по условию задачи величина уменьшается, перед процентом ставится минус. Если же величина увеличивается, ставим плюс.
С переменной k все понятно — это 10%, но что такое х? Давайте вернемся к условию задачи. Нам известно, что продавец делает скидку 10% от стоимости всей покупки. А мы совсем недавно убедились, что вся покупка нам обойдется в 540 рублей. Другими словами, х = 540, k = 10. Подставим эти числа в формулу:
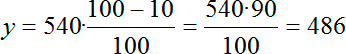
Это значит, что за 30 пирожков со скидкой 10% мы заплатим 489 рублей. Это именно то, что требовалось найти в задаче. Все, мы нашли ответ.
Переходим ко второй задаче:
Задача B2. Тетрадь стоит 64 рубля. Сколько рублей заплатит покупатель за 50 тетрадей, если при покупке больше 30 тетрадей магазин делает скидку 5% от стоимости всей покупки?
Очевидно, что данная задача полностью аналогична предыдущей, поэтому будем делать ее в том же порядке. В первую очередь, узнаем, сколько мы потратим на 50 тетрадей, если каждая стоит 64 рубля, причем не будем учитывать никакую скидку. Просто умножим 64 на 50:
S = 64 · 50 = 3200
Вот сколько мы потратим на 50 тетрадей без учета скидки. А теперь давайте учтем скидку с помощью нашей формулы:
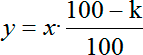
Обратите внимание: в числителе стоит именно (100 − k), потому что скидка означает, что исходная величина уменьшается. В роли исходного значения х выступает 3200, а k по условию задачи равно 5. Подставляем наши числа в формулу и получаем:
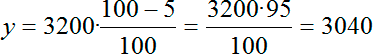
Когда исходная величина уменьшается, в формуле простого процента перед коэффициентом k ставится знак «минус».
Именно столько мы заплатим за 50 тетрадей с учетом скидки 5%. Это и есть ответ к задаче.
Вот и все. Мы только что дважды применили формулу простого процента для решения реальных задач с ЕГЭ по математике. На этом урок закончен.