Специфика работы с логарифмами в задаче B15

22 февраля 2012

Вообще говоря, для решения задачи B15 с логарифмом надо знать две формулы:

Первая формула — классическая производная натурального логарифма, вторая — производная сложной функции. Обратите внимание: в числителе стоит число k, это не опечатка.

Добавьте к этим формулам стандартные правила вычисления производных — и задача B15 решена:

(f ± g) ’ = f ’ ± g ’;
(c · f) ’ = c · f ’, c ∈ R.

В настоящих задачах логарифмы никогда не встречаются сами по себе. Поэтому обязательно приводите всю производную к общему знаменателю. Почему это важно, узнаете из примеров.

Задача. Найдите наименьшее значение функции на отрезке [0,5; 4]:

y = 2x² − 4 ln x + 5

Находим производную:

Выясняем, когда производная равна к нулю. Дробь равна нулю, когда ее числитель равен нулю. Имеем:

4(x² − 1) = 0;
x² = 1;
x = ±1.

Корень x = −1 не принадлежит отрезку [0,5; 4], поэтому нас интересует только x = 1. Кроме того, рассмотрим концы отрезка — числа 0,5 и 4. Итого три числа: 0,5; 1; 4. Поскольку требуется найти наименьшее значение функции, подставляем эти числа в исходную функцию:

y (0,5) = 2 · 0,5² − 4 ln 0,5 + 5 = 0,5 − 4 ln 0,5 + 5 = 5,5 − 4 ln 0,5;
y (1) = 2 · 1² − 4 ln 1 + 5 = 2 − 0 + 5 = 7;
y (4) = 2 · 4² − 4 ln 4 + 5 = 32 − 4 ln 4 + 5 = 37 − 4 ln 4.

В общем, выбирать особо не из чего. Ответ: 7. Потому что числа 5,5 − 4ln 0,5 и 37 − 4ln 4 иррациональны, их нельзя записать в виде конечной десятичной дроби.

Задача. Найдите точку минимума функции:

y = 2x − 5 ln (x − 7) + 3

Снова считаем производную:

Под логарифмом стоит линейная функция y = x − 7. Коэффициент при переменной x равен k = 1, поэтому в числителе никаких дополнительных множителей не возникнет — только множитель 5, который стоит перед логарифмом.

Поскольку требуется найти точку минимума, считаем нули числителя и знаменателя:

2x − 19 ⇒ x = 19 : 2 = 9,5;
x − 7 = 0 ⇒ x = 7.

Отмечаем эти точки на прямой, расставляем знаки производной между точками:

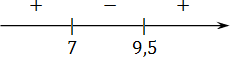
Итак, в точке x = 9,5 производная меняет знак с минуса на плюс, если считать слева — направо, в направлении стрелки. Это и есть точка минимума.

Задача. Найдите наибольшее значение функции на отрезке [−1,5; 1]:

y = 3 ln (x + 2) − 3x + 10

Считаем производную:

Находим нули числителя:

−3x − 3 = 0;
x = −1.

Нули знаменателя нас не интересуют, поскольку требуется найти значение функции. А когда знаменатель равен нулю, значение функции не определено.

Поскольку корень x = −1 ∈ [−1,5; 1], получаем три точки: −1,5; −1; 1. Подставляем их в исходную функцию:

y (−1,5) = 3 ln (−1,5 + 2) − 3 · (−1,5) + 10 = 3 ln 0,5 + 14,5;
y (−1) = 3 ln (−1 + 2) − 3 · (−1) + 10 = 3 ln 1 + 13 = 0 + 13 = 13;
y (1) = 3 ln (1 + 2) − 3 · 1 + 10 = 3 ln 3 + 7.

Понятно, что числа 3 ln 0,5 + 14,5 и 3 ln 3 + 7 нельзя записать в ответ. Остается только число 13 — это и будет наибольшее значение.

Вынесение степени за знак логарифма

Еще одна полезная фишка, которая избавит вас от сложных производных:

ln (f (x))^k = k · ln f (x)

Обратите внимание: в первом случае внутри логарифма стоит степень, для которой потребуется производная сложной функции. Во втором случае все намного проще, поскольку чаще всего f (x) — это обычная линейная функция.

Этот прием часто встречается в задачах на вычисление максимального и минимального значения. В задачах на точки экстремума его почти не применяют. Прежде чем решать такую задачу, обязательно найдите ОДЗ логарифма. Если забыли, что это такое, см. «Что такое логарифм».

Задача. Найдите наименьшее значение функции на отрезке [−4; 1]:

y = 5x − ln (x + 5)⁵

Итак, область допустимых значений логарифма — аргумент должен быть больше нуля. Имеем:

(x + 5)⁵ > 0;
x + 5 > 0;
x > −5;
x ∈ (−5; +∞).

Теперь решаем задачу. Сначала немного преобразуем исходное выражение:

y = 5x − 5 ln (x + 5)

Это и есть вынесение степени за знак логарифма. Считаем производную:

Дальше все стандартно. Нас интересует значение функции, поэтому приравниваем числитель к нулю:

5x + 20 = 0;
x = −4.

Полученное число x = −4 ∈ [−4; 1] совпадает с концом отрезка, поэтому кандидатов на наименьшее значение всего два: −4 и 1. Оба числа подходят по ОДЗ. Поскольку требуется найти наименьшее значение, подставляем эти числа в исходную функцию:

y (−4) = 5 · (−4) − 5 · ln (−4 + 5) = −20 − 5 · ln 1 = −20;
y (1) = 5 · 1 − 5 · ln (1 + 5) = 5 − 5 ln 6.

Второе число — точно не ответ, поскольку его нельзя представить в виде десятичного числа. Значит, наименьшее значение функции равно −20.

Задача. Найдите точку максимума функции:

y = 18 ln x − x² + 5

ОДЗ логарифма: x > 0 ⇒ x ∈ (0; +∞). Считаем производную:

Поскольку требуется найти точку максимума, нас интересует и числитель, и знаменатель. Приравниваем их к нулю:

2 · (9 − x²) = 0 ⇒ x² = 9 ⇒ x = ±3 — числитель;
x = 0 — знаменатель.

Получили три точки. Отмечаем эти точки и знаки производной на числовой прямой:

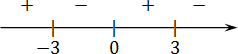
Требуется найти точку максимума — там, где плюс меняется на минус. Таких точек две: x = −3 и x = 3. Но вспомним ОДЗ: x ∈ (0; +∞). Значит, точка x = −3 не подходит. Остается точка x = 3 — это и будет ответ.

Смотрите также: