Предлагаю вашему вниманию решение настоящего варианта ЕГЭ-2011 по математике, который сдавали 6 июня. Здесь представлена только часть B — часть C будет разобрана отдельно. Изначально я хотел опубликовать их вместе, но информации оказалось так много, что лучше разбить ее на «порции».
По словам моих учеников, самыми тяжелыми оказались задачи B4, B9 и B12. Напротив, задачи B7 и B11, которые традиционно считаются сложными, решались без проблем. Задача B5, в которой надо много считать, вообще не вызвала ни у кого затруднений.
Задача. Спидометр автомобиля показывает скорость в милях в час. Какую скорость (в милях в час) показывает спидометр, если автомобиль движется со скоростью 68 км в час? (Считайте, что 1 миля равна 1,6 км)
Пусть спидометр показывает скорость x миль/ч. Имеем:
1 миля/ч — это 1,6 км/ч
x миль/ч — это 68 км/ч
Составим пропорцию:
Задача. На рисунке жирными точками показано суточное количество осадков, выпадавших в Элисте с 7 по 18 декабря 2001 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки соединены линией. Определите по рисунку, какого числа выпало ровно 1,5 мм осадков.
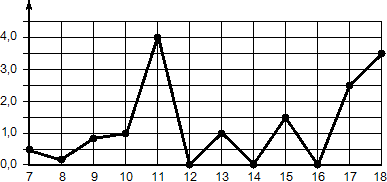
Если провести горизонтальную прямую на уровне 1,5 мм, то найдется ровно одна точка, лежащая на этой прямой. Эта точка — 15 декабря.

Задача. Решите уравнение:
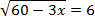
Возведем обе части уравнения в квадрат, получим:
60 − 3x = 36 ⇒ −3x = −24 ⇒ x = 8
Проверять корень на ОДЗ здесь не требуется, поскольку в уравнении присутствует лишь один радикал, и за его пределами переменных нет.
Задача. В треугольнике ABC проведена биссектриса AD. Угол C равен 62°, угол CAD равен 32°. Найдите угол B. Ответ дайте в градусах.
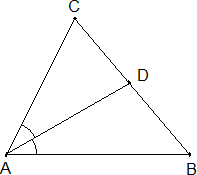
Поскольку AD — биссектриса,
Тогда
Поскольку сумма углов в треугольнике равна 180°, имеем:
Задача. Строительной фирме надо приобрести 50 кубометров строительного бруса у одного из трех поставщиков. Какова наименьшая стоимость такой покупки с доставкой (в рублях)? Цены и условия доставки приведены в таблице.
Поставщик Стоимость
пенобетона(руб. за 1 м2) Стоимость
доставки
в рубляхДополнительные
условияА 3500 9900 (нет) Б 4500 7000 При заказе на сумму больше 150 000 руб. доставка бесплатно В 3600 7900 При заказе на сумму больше 200 000 руб. доставка бесплатно
Найдем стоимость покупки для каждого поставщика.
Поставщик A:
Поставщик Б:
Поставщик В:
Минимальная цена — у первого поставщика. 184 900 рублей.
Задача. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см. Ответ дайте в квадратных сантиметрах.

Обведем треугольник в квадрат так, как показано на рисунке:

Площадь большого квадрата:
Площадь верхнего треугольника:
Площадь нижнего треугольника:
Искомая площадь:
Конечно, можно найти площадь намного проще, без вписывания треугольника в квадрат, но такой подход не универсален. Зато предложенный выше — универсален и работает для всех выпуклых фигур.
Задача. Найдите cos α, если известно следующее:
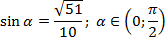
Поскольку α ∈ (0; π/2), это первая координатная четверть, где все синусы и косинусы положительны.
Основное тригонометрическое тождество:
Мы взяли положительный корень, потому что косинус в первой координатной четверти положителен.
Задача. На рисунке изображен график функции f(x) и касательная к этому графику
в точке x0. Найдите значение производной этой функциив точке x0. 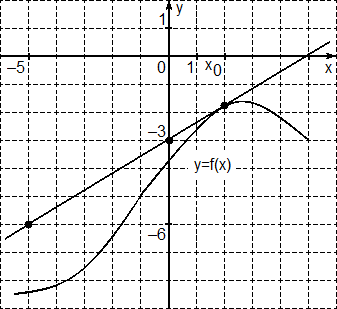
Рассмотрим две точки: A = (−5; −6) и B = (0; −3);
Эти точки лежат на касательной. Дальше все просто:
Δx = 0 − (−5) = 5;
Δy = −3 − (−6) = 3;
D = Δy/Δx = 3/5 = 0,6.
Задача. В цилиндрическом сосуде уровень жидкости достигает 64 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 4 раза больше диаметра первого?
Основная формула:
Поскольку объем не меняется,
Итак, по оси Z размер уменьшится в 16 раз. Изначально он был равен 64. Получаем:
Задача. В ходе распада радиоактивного вещества изотопа его масса уменьшается по закону:
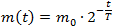
где m0 — начальная масса изотопа,
t (мин.) — время, прошедшее от начального момента,T (мин) — период полураспада. В начальный момент времени масса изотопаm0 = 400 мг. Период его полураспадаT = 5 мин. Через сколько минут масса изотопа будет равна 25 мг?
Это задача с функцией. Известны следующие величины:
m0 = 400; T = 5; m(t) = 25.
Подставляем — получаем обычное показательное уравнение:
Задача. Найдите наибольшее значение функции
y = x3 + 7x2 + 8x − 8 на отрезке [−6; −3].
Для начала найдем производную:
Найдем нули производной:
Поскольку корень x = −2/3 не лежит на отрезке [−6; −3], нас интересует только
Итак, у нас есть три точки: −6; −4; −3. Первые две являются концами отрезка, последняя — нулем производной и, следовательно, кандидатом на экстремум. Вычислим значение функции в каждой из них:
y(−6) = −20; y(−3) = 4; y(−4) = 8;
Требуется выбрать наибольшее — это число 8.
Задача. Лодка в 9:00 вышла из пункта А в пункт Б, расположенный в 15 км от А. Пробыв в пункте Б 2 часа, лодка отправилась назад и вернулась в пункт А в 19:00 того же дня. Определите (в км/ч) собственную скорость лодки, если известно, что скорость течения равна 1 км/ч.
Пусть собственная скорость лодки равна x км/ч. Тогда по течению она идет со скоростью
Всего лодка была в пути 19 − 9 = 10 часов. Но из этих 10 часов она 2 часа стояла в пункте Б, поэтому реально в пути она была только 10 − 2 = 8 часов.
Расстояние между пунктами по течению лодка пройдет
15x · 1 = 4 · (x2 − 1) ⇒ 4x2 − 15x − 4 = 0
Последнее квадратное уравнение имеет два корня:
Вот и все. Это была часть B. Часть C — на подходе.