Сегодня мы разберем самый простой прием, который используется в задаче B5 ЕГЭ по математике для нахождения площадей фигур, начерченных на координатной сетке. Этот метод также известен как метод описанного прямоугольника.
Рассмотрим самый простой случай:
Для работы нам потребуются две формулы:
Итак, задача B5 из реального ЕГЭ по математике:
Задача B5. Найдите площадь пятиугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см. Ответ дайте в квадратным сантиметрах.

В первую очередь строим описанный прямоугольник, причем так, чтобы на каждой из его сторон находилась хотя бы одна из сторон исходной фигуры.
В нашем случае оказалось, что три вершины исходной фигуры действительно лежат на сторонах описанного прямоугольника. А вот две оставшиеся лежат внутри красного периметра, поэтому для них требуется дополнительное построение. Проведем из каждой вершины высоты к ближайшим сторонам:

Готово! Мы получили прямоугольник, внутри которого заключена наша фигура, а также 7 маленьких фигур, чьи площади считаются по формулам прямоугольного треугольника и прямоугольника. Эти дополнительные фигуры называются разбиением.
Давайте обозначим площади этих фигур: S1, S2, S3, S4, S5, S6 и S7. Получим следующую картинку:
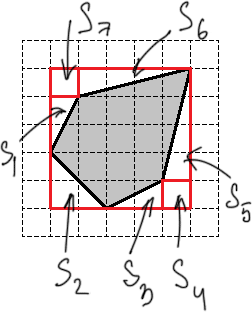
Теперь считаем каждую из обозначенных площадей. Имеем:
S1 = 0,5 · 1 · 2 = 1;
S2 = 0,5 · 2 · 2 = 2;
S3 = 0,5 · 1 · 2 = 1;
S4 = 1 · 1 = 1;
S5 = 0,5 · 4 · 1 = 2;
S6 = 0,5 · 1 · 4 = 2;
S7 = 1 · 1 = 1.
Далее считаем общую площадь красного прямоугольника. На самом деле это квадрат, каждая сторона которого равна 5. Итого площадь равна:
S0 = 5 · 5 = 25
Теперь осталось найти площадь закрашенной фигуры — ту самую, которую от нас и просят найти в задаче B5 ЕГЭ по математике. Для этого из общей площади S0 надо вычесть площади тех кусочков S1, S2, ..., S7, которые мы только что считали. Получим:
S = S0 − (S1 + S2 + ... + S7) = 25 − (1 + 2 + ... + 1) = 25 − 10 = 15
Вот и все решение! Площадь закрашенной фигуры равна 15. Надеюсь, этот урок будет полезен тем, кто начинает готовиться к ЕГЭ по математике.