В этом уроке мы рассмотрим, как с помощью определителя составить уравнение плоскости. Если вы не знаете, что такое определитель, зайдите в первую часть урока — «Матрицы и определители». Иначе вы рискуете ничего не понять в сегодняшнем материале.
Зачем вообще нужно уравнение плоскости? Все просто: зная его, мы легко высчитаем углы, расстояния и прочую хрень в задаче C2. В общем, без этого уравнения не обойтись. Поэтому сформулируем задачу:
Задача. В пространстве даны три точки, не лежащие на одной прямой. Их координаты:
M = (x1, y1, z1);
N = (x2, y2, z2);
K = (x3, y3, z3);Требуется составить уравнение плоскости, проходящей через эти три точки. Причем уравнение должно иметь вид:
Ax + By + Cz + D = 0
где числа A, B, C и D — коэффициенты, которые, собственно, и требуется найти.
Ну и как получить уравнение плоскости, если известны только координаты точек? Самый простой способ — подставить координаты в уравнение
Многие ученики считают такое решение крайне утомительным и ненадежным. Прошлогодний ЕГЭ по математике показал, что вероятность допустить вычислительную ошибку действительно велика.
Поэтому наиболее продвинутые учителя стали искать более простые и изящные решения. И ведь нашли! Правда, полученный прием скорее относится к высшей математике. Лично мне пришлось перерыть весь Федеральный перечень учебников, чтобы убедиться, что мы вправе применять этот прием
Хватит лирики, приступаем к делу. Для начала — теорема о том, как связаны определитель матрицы и уравнение плоскости.
Теорема. Пусть даны координаты трех точек, через которые надо провести плоскость:
M = (x1, y1, z1); N = (x2, y2, z2); K = (x3, y3, z3). Тогда уравнение этой плоскости можно записать через определитель: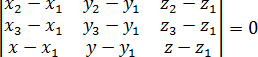
Для примера попробуем найти пару плоскостей, которые реально встречаются в задачах С2. Взгляните, как быстро все считается:
Задача. Составьте уравнение плоскости, проходящей через точки:
A1 = (0, 0, 1);
B = (1, 0, 0);
C1 = (1, 1, 1);
Составляем определитель и приравниваем его к нулю:
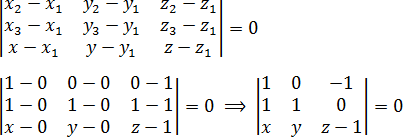
Раскрываем определитель:
a = 1 · 1 · (z − 1) + 0 · 0 · x + (−1) · 1 · y = z − 1 − y;
b = (−1) · 1 · x + 0 · 1 · (z − 1) + 1 · 0 · y = −x;
d = a − b = z − 1 − y − (−x) = z − 1 − y + x = x − y + z − 1;
d = 0 ⇒ x − y + z − 1 = 0;
Как видите, при расчете числа d я немного «причесал» уравнение, чтобы переменные
Задача. Составьте уравнение плоскости, проходящей через точки:
A = (0, 0, 0);
B1 = (1, 0, 1);
D1 = (0, 1, 1);
Сразу подставляем координаты точек в определитель:
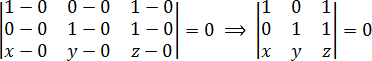
Снова раскрываем определитель:
a = 1 · 1 · z + 0 · 1 · x + 1 · 0 · y = z;
b = 1 · 1 · x + 0 · 0 · z + 1 · 1 · y = x + y;
d = a − b = z − (x + y) = z − x − y;
d = 0 ⇒ z − x − y = 0 ⇒ x + y − z = 0;
Итак, уравнение плоскости снова получено! Опять же, на последнем шаге пришлось поменять в нем знаки, чтобы получить более «красивую» формулу. Делать это в настоящем решении совсем не обязательно,
Как видите, составлять уравнение плоскости теперь намного проще. Подставляем точки в матрицу, считаем определитель — и все, уравнение готово.
На этом можно было бы закончить урок. Однако многие ученики постоянно забывают, что стоит внутри определителя. Например, в какой строчке стоит
Итак, разбираемся, откуда возникает такое суровое уравнение с определителем. Это поможет вам запомнить его и успешно применять.
Все плоскости, которые встречаются в задаче C2, задаются тремя точками. Эти точки всегда отмечены на чертеже, либо даже указаны прямо в тексте задачи. В любом случае, для составления уравнения нам потребуется выписать их координаты:
M = (x1, y1, z1);
N = (x2, y2, z2);
K = (x3, y3, z3).
Рассмотрим еще одну точку на нашей плоскости с произвольными координатами:
T = (x, y, z)
Берем любую точку из первой тройки (например,
MN = (x2 − x1, y2 − y1, z2 − z1);
MK = (x3 − x1, y3 − y1, z3 − z1);
MT = (x − x1, y − y1, z − z1).
Теперь составим из этих векторов квадратную матрицу и приравняем ее определитель к нулю. Координаты векторов станут строчками матрицы — и мы получим тот самый определитель, который указан в теореме:
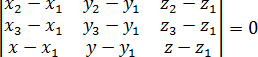
Эта формула означает, что объем параллелепипеда, построенного на векторах
У определителей есть несколько замечательных свойств, которые еще более упрощают решение задачи C2. Например, нам неважно, из какой точки проводить векторы. Поэтому следующие определители дают такое же уравнение плоскости, как и приведенный выше:
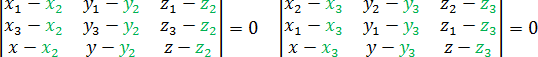
Также можно менять местами строчки определителя. Уравнение при этом останется неизменным. Например, многие любят записывать строчку с координатами точки
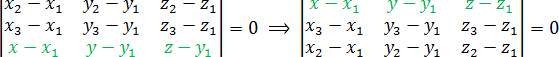
Некоторых смущает, что в одной из строчек присутствуют переменные
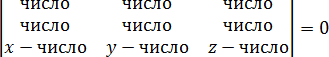
Затем определитель раскрывается по схеме, приведенной в начале урока, и получается стандартное уравнение плоскости:
Ax + By + Cz + D = 0
Взгляните на пример. Он последний в сегодняшнем уроке. Я специально поменяю строчки местами, чтобы убедиться, что в ответе получится одно и то же уравнение плоскости.
Задача. Составьте уравнение плоскости, проходящей через точки:
B1 = (1, 0, 1);
C = (1, 1, 0);
D1 = (0, 1, 1).
Итак, рассматриваем 4 точки:
B1 = (1, 0, 1);
C = (1, 1, 0);
D1 = (0, 1, 1);
T = (x, y, z).
Для начала составим стандартный определитель и приравниваем его к нулю:
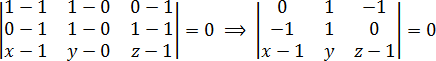
Раскрываем определитель:
a = 0 · 1 · (z − 1) + 1 · 0 · (x − 1) + (−1) · (−1) · y = 0 + 0 + y;
b = (−1) · 1 · (x − 1) + 1 · (−1) · (z − 1) + 0 · 0 · y = 1 − x + 1 − z = 2 − x − z;
d = a − b = y − (2 − x − z) = y − 2 + x + z = x + y + z − 2;
d = 0 ⇒ x + y + z − 2 = 0;
Все, мы получили ответ:
Теперь давайте переставим пару строк в определителе и посмотрим, что произойдет. Например, запишем строчку с переменными
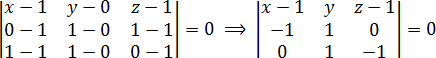
Вновь раскрываем полученный определитель:
a = (x − 1) · 1 · (−1) + (z − 1) · (−1) · 1 + y · 0 · 0 = 1 − x + 1 − z = 2 − x − z;
b = (z − 1) · 1 · 0 + y · (−1) · (−1) + (x − 1) · 1 · 0 = y;
d = a − b = 2 − x − z − y;
d = 0 ⇒ 2 − x − y − z = 0 ⇒ x + y + z − 2 = 0;
Мы получили точно такое же уравнение плоскости:
Итак, мы убедились, что уравнение плоскости не зависит от последовательности строк. Можно провести аналогичные вычисления и доказать, что уравнение плоскости не зависит и от точки, координаты которой мы вычитаем из остальных точек.
В рассмотренной выше задаче мы использовали точку