Сегодня мы разберем очень простой и — не побоюсь этого слова — красивый прием, с помощью которого составляется уравнение плоскости в задаче C2 из ЕГЭ по математике. Урок разделен на две части: теоретическую (что такое определитель и как его считать) и практическую (как с помощью определителя находить уравнение плоскостей). Те, кому не терпится, могут сразу перейти ко второй части — «Уравнение плоскости через определитель».
Если вы до сих пор не сталкивались с определителями, не расстраивайтесь — сегодня мы разберем все, что надо знать об этих объектов для решения задачи C2. А если кто-то из учителей (особенно на пробниках) будет возникать, мол, этого нет в школьной программе, пошлите их читать учебник Калинина «Геометрия 10—11 классы». В этой замечательной книге (довольно объёмной и содержательной, между прочим) все подробно расписано на стр. 450. Итак, поехали!
В этом уроке не будет строгих определений из высшей математики. Потому что они крайне сложны для понимания. Лучше определим их вот как:
Примеры квадратных матриц размером 2x2, 3x3 и 4x4:
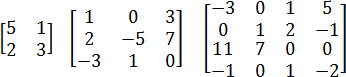
Примеры прямоугольных матриц 2x3, 3x2 и даже 4x1:
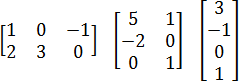
Как видите, матрицы бывают разных размеров и обозначаются квадратными скобкам. Внутри них могут стоять совершенно разные числа, в т.ч. отрицательные и нули. Но для решения задачи C2 нам потребуются только квадратные матрицы размером 3x3. Например, такие:
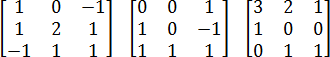
Теперь разберемся с определителями. Чаще всего их обозначают буквой d (от слова determinant). Поскольку нас интересуют только матрицы 3x3, учимся считать определители именно для них. Процедура выглядит довольно просто. Взгляните на картинку:
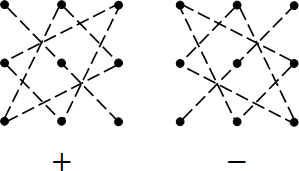
Что это за пентаграммы? На первом рисунке мы берем три числа, лежащие на диагонали, и перемножаем их. Затем берем другие тройки чисел, лежащие в вершинах треугольников, и тоже перемножаем их между собой. В результате всех этих махинаций мы получим три числа, которые надо сложить (поэтому внизу левой картинки стоит знак плюс).
Теперь разбираемся со второй картинкой. Здесь мы снова берем и перемножаем три числа, но уже на другой диагонали. Так же мы снова берем два треугольника и перемножаем числа, стоящие в их углах (отдельно для каждого треугольника). Полученные три числа опять складываем, а результат вычитаем из первого числа (поэтому внизу справа стоит знак минус).
На первый взгляд, без бутылки не разберешься. Но на практике такие определители считаются очень быстро. Некоторые даже умудряются считать их устно. Чтобы убедиться в этом, давайте попробуем найти пару определителей.
Задача. Найдите определитель квадратной матрицы:
Перемножаем числа. стоящие на первой диагонали (выходит из левого верхнего угла):
1 · 5 · 9 = 45
Теперь перемножаем числа, стоящие в вершинах треугольников на первом рисунке. Каждую тройку надо считать отдельно:
2 · 6 · 7 = 84;
3 · 4 · 8 = 96.
Осталось сложить полученные числа:
45 + 84 + 96 = 225
Итак, для первого рисунка (отмеченного знаком плюс) мы получили число a = 225.
Переходим ко второй диагонали набору треугольников. Эта диагональ начинается из правого верхнего угла матрицы. Имеем:
3 · 5 · 7 = 105
Выписываем числа из двух оставшихся треугольников:
2 · 4 · 9 = 72;
1 · 6 · 8 = 48;
Осталось выполнить последние шаги — сложить эти три числа, а полученное число (назовем его b) вычесть из числа a = 225, найденного ранее:
b = 105 + 72 + 48 = 225;
d = a − b = 225 − 225 = 0.
Получили число d = 0 — это и есть определитель.
Задача. Найдите определитель квадратной матрицы:
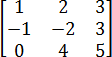
В этот раз не будем подробно расписывать каждый шаг. Запишем только то, что действительно надо писать в решении. А именно:
a = 1 · (−2) · 5 + 2 · 3 · 0 + 3 · (−1) · 4 = −10 + 0 − 12 = −22;
b = 3 · (−2) · 0 + 2 · (−1) · 5 + 1 · 3 · 4 = 0 − 10 + 12 = 2;
d = a − b = −22 − 2 = −24.
Вот и все! Число d = −24 — это ответ.
Задача. Найдите определитель квадратной матрицы:
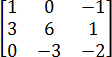
Снова запишем только вычисления:
a = 1 · 6 · (−2) + 0 · 1 · 0 + (−1) · 3 · (−3) = −12 + 0 + 9 = −3;
b = (−1) · 6 · 0 + 1 · 1 · (−3) + 0 · 3 · (−2) = 0 − 3 + 0 = −3;
d = a − b = −3 − (−3) = −3 + 3 = 0.
Из первой и последней задачи следует, что определитель матрицы вполне может равняться нулю. Это свойство как раз и потребуется для решения задачи C2. Точнее, для того, чтобы быстро составлять уравнения плоскостей.
Ну и как составлять эти уравнения? Ответ смотрите во второй части — «Уравнение плоскости через определитель».