Решая задачи B12, многие ученики допускают одну и ту же ошибку. Вместо того чтобы просто подставить коэффициенты в уравнение и найти ответ, они начинают смотреть на единицы измерения — градусы, метры, проценты и т.д.
Нелишним будет напомнить, что B12 — задача с практическим содержанием, и единицы измерения здесь будут всегда. Никакой смысловой нагрузки они не несут, поэтому запомните следующее правило:
Единицы измерения в задаче B12 писать не надо. Если они присутствуют в формуле изначально — удалите их. Все уравнения должны содержать только числа — никаких метров, градусов и рублей.
Так вы сэкономите время и убережете себя от многих ошибок. Заодно получите более «чистое» и наглядное уравнение, которое легче решается.
Задача. Осадная машина метает камни под определенным углом к горизонту с фиксированной начальной скоростью. Траектория полета камня описывается формулой:
y = ax2 + bx
где a = −1/50 м−1, b = 1 — постоянные параметры,x — расстояние от машины до камня по горизонтали,y — высота камня над землей.На каком наименьшем расстоянии от крепостной стены высотой 12 метров надо расположить машину, чтобы камни пролетали над ней на высоте не менее 1 метра? Ответ выразите в метрах.
Здесь все просто: коэффициенты выражены в метрах, других единиц измерения нет. Поэтому спокойно зачеркиваем
Правильно:
13 = (−1/50) · x2 + x;
Неправильно:
13 м = (−1/50 м−1) · x2 + x.
Задача. Зависимость температуры (в градусах Кельвина) от времени (в минутах) для нагревательного элемента некоторого прибора вычисляется по формуле:
T(t) = T0 + bt + at2
где T0 = 1400 К, a = −20 К/мин, b = 150 К/мин2. Известно, что при температуре более 2000 К прибор может испортиться, и его надо отключить. Определите (в минутах), через какое наибольшее время после начала работы надо отключить прибор.
По условию, температура измеряется в градусах Кельвина, время — в минутах. Других единиц измерения в задаче нет, дополнительных преобразований не требуется, поэтому подставляем числа в уравнение.
Правильно:
2000 = 1400 + 150t − 20t2;
Неправильно:
2000 К = 1400 К + 150t − 20t2.
Задача. При температуре 0 °С рельс имеет длину
l0 = 12 метров. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону:l(t°) = l0 · (1 + a · t°)
где a = 1,2 · 10−5 (°C)−1 — коэффициент теплового расширения,t° — температура (в градусах Цельсия).При какой температуре рельс удлинится на 6 мм? Ответ выразите в градусах Цельсия.
В задаче присутствуют сразу три единицы измерения: метры, миллиметры и градусы Цельсия. Переведем миллиметры в метры:
Кроме того, единицы измерения присутствуют в самой формуле. Непонятно, зачем составители задач пишут
Правильно:
12 + 6 · 10−3 = 12 · (1 + 1,2 · 10−5 · t);
Неправильно:
12 м + 6 мм = 12 м · (1 + 1,2 · 10−5 · t°);
6 мм = 12 м · (1 + 1,2 · 10−5 · t°).
Задача. Коэффициент полезного действия (КПД) двигателя вычисляется по формуле:
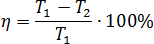
где T1 — температура нагревателя (в градусах Кельвина),T2 — температура холодильника (в градусах Кельвина).Определите наименьшую температуру
нагревателя T1, при которой КПД составит не менее 75%, если температура холодильникаT2 = 300 К. Ответ выразите в градусах Кельвина.
Итак, в задаче есть две единицы измерения: градусы Кельвина и проценты.
Правильно:
Неправильно:
Задача. Для определения эффективной температуры звезд используют закон Стефана — Больцмана, согласно которому мощность излучения нагретого тела прямо пропорциональна площади его поверхности и четвертой степени температуры:
P = σST 4
где σ = 5,7 · 10−8 — постоянная, площадь измеряется в квадратных метрах, температура — в градусах Кельвина, а мощность — в ваттах.Известно, что некоторая звезда имеет площадь
S = 4 · 1010 м2, а излучаемая еюмощность P не менее22,8 · 1021 Вт. Определите наименьшую возможную температуру этой звезды. Ответ дайте в градусах Кельвина.
Градусы Кельвина, квадратные метры и ватты — стандартные единицы измерения, которые спокойно можно отбросить.
Правильно:
22,8 · 1021 = 5,7 · 10−8 · 4 · 1010 T 4;
Неправильно:
22,8 · 1021 Вт = 5,7 · 10−8 · 4 · 1010 м2 · T 4.
Думаю, смысл понятен. Множество ошибок допускается
Отдельная тема — экономические задачи, где приходится работать с большими числами. Увидев аббревиатуру «тыс. руб.», многие приписывают к исходным коэффициентам лишние нули, чего делать категорически нельзя. Взгляните на примеры:
Задача. Зависимость объема спроса q (единиц в месяц) на продукцию предприятия-монополиста
от цены p (тыс. руб.) задается формулой:q = 200 − 10p. Выручка предприятияза месяц r (тыс. руб.) задается формулойr(p) = q · p. Определите наибольшую
цену p, при которой месячнаявыручка r(p) составит не менее 800 тыс. руб. Ответ приведите в тыс. руб.
В задаче снова присутствуют две величины: количество товара и его цена. Загадочные «тыс. руб.» являются обычной единицей измерения — такой же, как штуки, метры и градусы. При подстановке в уравнение «тыс. руб.» можно спокойно зачеркнуть — числа при этом не изменятся.
Правильно:
800 = (200 − 10p) · p;
Неправильно:
800 тыс. руб. = (200 − 10p) · p;
800 000 = (200 − 10p) · p.
Задача. Ежемесячная прибыль фирмы рассчитывается по формуле:
π(q) = q(p − v) − f
Фирма продает свою продукцию по цене
p = 1200 руб. за штуку, переменные издержки на ее производство составляютv = 600 руб. за штуку, постоянные издержкиf = 1 400 000 руб. Определите наименьший месячный объем производства
q (шт.), при котором прибыль составит не менее 1 000 000 руб. в месяц.
В принципе, здесь все стандартно: есть цена и объем производства. Смущают разве что большие числа. Все цены даны в рублях, при подстановке в уравнение аббревиатуру «руб.» можно спокойно зачеркнуть.
Неправильно:
1 000 000 руб. = q · (1200 − 600) − 1 400 000 руб.;
1000 тыс. руб. = q · (1200 − 600) − 1400 тыс. руб.;
1 млн. руб. = q · (1200 − 600) − 1,4 млн. руб.
Сказанное выше не отменяет другого важного правила: для всех величин должна применяться единая система измерения. Так, в задачах про рельсы длина этого самого рельса выражается в метрах, а удлинение — в миллиметрах. Прежде чем составлять уравнение, надо перевести все в метры.
Все числа должны быть переведены в единую систему измерения. И лишь затем можно составить уравнение, где единиц измерения не будет вообще.
Подобные задачи редко встречаются на ЕГЭ по математике, но уж если встретятся — мало не покажется. Поэтому рассмотрим еще раз задачу с рельсами:
Задача. При температуре 0 °С рельс имеет длину
l0 = 20 метров. При строительстве железной дороги между рельсами оставили зазор в 9 мм. Когда температура растет, начинается тепловое расширение рельса, и его длина вычисляется по формуле:l(t) = l0 · (1 + a · t)
где a = 1,2 · 10−5 (°C)−1 — коэффициент теплового расширения,t — температура (в градусах Цельсия). При какой минимальной температуре зазор между рельсами исчезнет? Ответ дайте в градусах Цельсия.
Основная проблема в том, что длина рельса измеряется в метрах, а зазор — в миллиметрах. Переведем все в метры: если 1000 мм = 1 м, то 9 мм =
Теперь подумаем: что значит «зазор между рельсами исчезнет»? Очевидно, это произойдет в тот момент, когда рельс удлинится на величину зазора, поэтому искомая длина рельса равна
Правильно:
20 + 0,009 = 20 · (1 + 0,000012 · t);
20 + 9 · 10−3 = 20 · (1 + 1,2 · 10−5 · t);
Неправильно:
20 м + 0,009 = 20 м · (1 + 1,2 · 10−5 · t);
20 м + 9 мм = 20 м · (1 + 1,2 · 10−5 · t).
Обратите внимание на коэффициенты. Их можно записать по-разному:
Всем своим ученикам я настоятельно рекомендую записывать числа именно в стандартном виде. Это очень просто и экономит много времени. А некоторые задачи (например, температура звезд) по-другому вообще не решаются.