Приведение дробей к общему знаменателю

27 июля 2011

Изначально я хотел включить методы приведения к общему знаменателю в параграф «Сложение и вычитание дробей». Но информации оказалось так много, а важность ее столь велика (ведь общие знаменатели бывают не только у числовых дробей), что лучше изучить этот вопрос отдельно.

Итак, пусть у нас есть две дроби с разными знаменателями. А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:

Дробь не изменится, если ее числитель и знаменатель умножить на одно и то же число, отличное от нуля.

Таким образом, если правильно подобрать множители, знаменатели у дробей сравняются — этот процесс называется приведением к общему знаменателю. А искомые числа, «выравнивающие» знаменатели, называются дополнительными множителями.

Для чего вообще надо приводить дроби к общему знаменателю? Вот лишь несколько причин:

1. Сложение и вычитание дробей с разными знаменателями. По-другому эту операцию никак не выполнить;
2. Сравнение дробей. Иногда приведение к общему знаменателю значительно упрощает эту задачу;
3. Решение задач на доли и проценты. Процентные соотношения являются, по сути, обыкновенными выражениями, которые содержат дроби.

Есть много способов найти числа, при умножении на которые знаменатели дробей станут равными. Мы рассмотрим лишь три из них — в порядке возрастания сложности и, в некотором смысле, эффективности.

Умножение «крест-накрест»

Самый простой и надежный способ, который гарантированно выравнивает знаменатели. Будем действовать «напролом»: умножаем первую дробь на знаменатель второй дроби, а вторую — на знаменатель первой. В результате знаменатели обеих дробей станут равными произведению исходных знаменателей. Взгляните:

Задача. Найдите значения выражений:

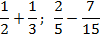
В качестве дополнительных множителей рассмотрим знаменатели соседних дробей. Получим:

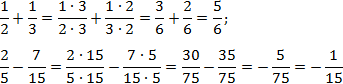
Да, вот так все просто. Если вы только начинаете изучать дроби, лучше работайте именно этим методом — так вы застрахуете себя от множества ошибок и гарантированно получите результат.

Единственный недостаток данного метода — приходится много считать, ведь знаменатели умножаются «напролом», и в результате могут получиться очень большие числа. Такова расплата за надежность.

Метод общих делителей

Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он достаточно редко. Метод заключается в следующем:

1. Прежде, чем действовать «напролом» (т.е. методом «крест-накрест»), взгляните на знаменатели. Возможно, один из них (тот, который больше), делится на другой.
2. Число, полученное в результате такого деления, будет дополнительным множителем для дроби с меньшим знаменателем.
3. При этом дробь с большим знаменателем вообще не надо ни на что умножать — в этом и заключается экономия. Заодно резко снижается вероятность ошибки.

Задача. Найдите значения выражений:

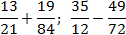
Заметим, что 84 : 21 = 4; 72 : 12 = 6. Поскольку в обоих случаях один знаменатель делится без остатка на другой, применяем метод общих множителей. Имеем:

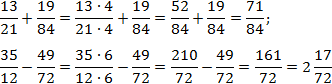
Заметим, что вторая дробь вообще нигде ни на что не умножалась. Фактически, мы сократили объем вычислений в два раза!

Кстати, дроби в этом примере я взял не случайно. Если интересно, попробуйте сосчитать их методом «крест-накрест». После сокращения ответы получатся такими же, но работы будет намного больше.

В этом и состоит сила метода общих делителей, но, повторюсь, применять его можно лишь в том случае, когда один из знаменателей делится на другой без остатка. Что бывает достаточно редко.

Метод наименьшего общего кратного

Когда мы приводим дроби к общему знаменателю, мы по сути пытаемся найти такое число, которое делится на каждый из знаменателей. Затем приводим к этому числу знаменатели обеих дробей.

Таких чисел очень много, и наименьшее из них совсем не обязательно будет равняться прямому произведению знаменателей исходных дробей, как это предполагается в методе «крест-накрест».

Например, для знаменателей 8 и 12 вполне подойдет число 24, поскольку 24 : 8 = 3; 24 : 12 = 2. Это число намного меньше произведения 8 · 12 = 96.

Наименьшее число, которое делится на каждый из знаменателей, называется их наименьшим общим кратным (НОК).

Обозначение: наименьшее общее кратное чисел a и b обозначается НОК(a; b). Например, НОК(16; 24) = 48; НОК(8; 12) = 24.

Если вам удастся найти такое число, итоговый объем вычислений будет минимальным. Посмотрите на примеры:

Задача. Найдите значения выражений:

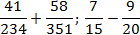
Заметим, что 234 = 117 · 2; 351 = 117 · 3. Множители 2 и 3 взаимно просты (не имеют общих делителей, кроме 1), а множитель 117 — общий. Поэтому НОК(234; 351) = 117 · 2 · 3 = 702.

Аналогично, 15 = 5 · 3; 20 = 5 · 4. Множители 3 и 4 взаимно просты, а множитель 5 — общий. Поэтому НОК(15; 20) = 5 · 3 · 4 = 60.

Теперь приведем дроби к общим знаменателям:

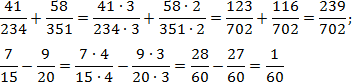
Обратите внимание, насколько полезным оказалось разложение исходных знаменателей на множители:

1. Обнаружив одинаковые множители, мы сразу вышли на наименьшее общее кратное, что, вообще говоря, является нетривиальной задачей;
2. Из полученного разложения можно узнать, каких множителей «не хватает» каждой из дробей. Например, 234 · 3 = 702, следовательно, для первой дроби дополнительный множитель равен 3.

Чтобы оценить, насколько колоссальный выигрыш дает метод наименьшего общего кратного, попробуйте вычислить эти же примеры методом «крест-накрест». Разумеется, без калькулятора. Думаю, после этого комментарии будут излишними.

Не думайте, что таких сложных дробей в настоящих примерах не будет. Они встречаются постоянно, и приведенные выше задачи — не предел!

Единственная проблема — как найти этот самый НОК. Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Здесь мы не будем этого касаться.

1. Сложение и вычитание дробей
2. Тест к уроку «Что такое числовая дробь» (средний)
3. Тест к уроку «Простые проценты» (легкий)
4. Метод узлов в задаче B5
5. Процент: неизвестно начальное значение (метод пропорции)
6. Задача B14: движение навстречу