Этим видео я начинаю целую серию видеоуроков по решению задач B2 на проценты. Мы разберем все — от самых простых задач (таких, как сегодня) до настоящей жести, которая, тем не менее, встречается на настоящем ЕГЭ по математике.
Сегодняшний урок посвящен самым простым задачам B2 и, соответственно, самому простому методу вычисления процентов. А именно, речь пойдет о методе пропорций.
Давайте приступим. Первая задача:
Задача. В школе 204 ученика изучают французский язык, что составляет 24% от числа всех учеников. Сколько учеников учится в школе?
Итак, решаем эту задачу. Переводим ее условие на язык пропорций.
Что нам известно? Нам даны 204 ученика, которые составляют 24% от всех учеников школы. Так и запишем:
204 — 25%
При этом в задаче спрашивается: сколько всего учеников учится в этой школе? Т.е. от нас требуется найти некоторое число x учеников, которое было бы равно общему количеству учеников школы, т.е. 100%. Запишем это:
x — 100%
В результате этих размышлений мы получили по сути таблицу размером 2 × 2, вмещающую в себя все условие задачи:
204 — 25%
x — 100%
Давайте составим из нее пропорцию:
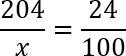
По сути, мы просто добавили дробную черту к приведенной выше конструкции и получили уравнение. Что ж, давайте его решать. Очевидно, что дробь, стоящая справа может быть сокращена: 24 : 4 = 6; 100 : 4 = 25. Перепишем еще раз полученную конструкцию:
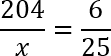
Теперь воспользуемся основным свойством пропорции (произведение крайних членов равно произведению средних членов) и перемножим наши числа крест-накрест. Получим:
204 · 25 = 6 · x
Обратите внимание: между полученными произведениями стоит знак равенства! Не сложение и не вычитание, как думаю многие ученики, а именно равенство. Решаем полученное уравнение:
x = 204 · 25 : 6 = 34 · 25 = 34 · (10 + 10 + 5) = 340 + 340 + 170 = 850
Как вы заметили, мы не стали перемножать числа 34 и 25 столбиком, а просто заметили, что 25 = 10 + 10 + 5, а затем раскрыли скобки.
Итак, мы получили, что x = 850. Это число и является ответом на вопрос, поставленный в задаче: сколько всего учеников учатся в школе. Таких учеников учится 850. Все, задача решена.
Переходим к следующей задаче:
Задача. 108 выпускников школы собираются учиться в технических вузах. Они составляют 40% от числа выпускников. Сколько в школе выпускников?
Как видим, это снова задача на проценты, и мы снова решаем ее методом пропорций.
Первый шаг. По условию, у нас есть 108 выпускников, которые составляют 40% от общего количества выпускников в школе. А нам надо найти x выпускников, которые составят 100%, т.е. все население школы, которое является выпускниками. Запишем это в виде соотношений:
108 — 40%
x — 100%
Что ж, снова составляем пропорцию. Делим первые два числа друг на друга и вторые два числа друг на друга. Полученные дроби приравниваем:
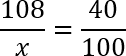
Дробь справа хорошо сокращается (как минимум, на 10). Можно было бы сократить еще и на 2, но дальше нам надо будет перемножать числа согласно основному свойству пропорции. Думаю, что умножить 108 на 10 будет гораздо проще, чем 108 на 5. Умножаем и получаем:
4x = 108 · 10;
4x = 1080.
Осталось решить полученное уравнение, т.е. разделить обе его стороны на 4. Получим:
x = 1080 : 4 = (1000 + 80) : 4 = 250 + 20 = 270
С помощью небольшой хитрости можно делить довольно большие числа без всяких уголков. Вот мы и получили ответ. Всего в школе 270 выпускников.
Как видите, с помощью метода пропорций задачи на проценты решаются очень и очень просто. Единственное, на что хотелось бы обратить внимание — это оформление самих решений. Взгляните: мы везде пишем, что некоторое число — это столько-то процентов. И нигде ни в коем случае не применяем знак равенства.
Это делается неслучайно. Потому что в противном случае мы бы получили выражения вида (на примере последней задачи):
108 = 40
Очевидно, что данное равенство неверно. Как следствие, такая интерпретация условия является некорректной.
В общем, при решении задач на проценты никогда так не пишите. Лучше потратить несколько дополнительных секунд и записать условие правильно, корректно, из которого легко следует пропорция, которая затем не менее легко решается:
108 — 40%
Надеюсь, этот урок поможет тем, кто готовится к ЕГЭ по математике или просто разбирается с задачами на проценты. А у меня на это все. До новых встреч!