Второй урок по комплексным числам. Если вы только начинаете изучать эту тему (что такое комплексная единица, модуль, сопряжённые), см. первый урок: «Что такое комплексное число».
Сегодня мы узнаем:
Начнём с ключевого определения.
Определение. Тригонометрическая форма комплексного числа — это выражение вида
\[z=\left| z \right|\cdot \left( \cos \text{ }\!\!\varphi\!\!\text{ }+i\sin \text{ }\!\!\varphi\!\!\text{ } \right)\]
где $\left| z \right|$ — модуль комплексного числа, $\text{ }\!\!\varphi\!\!\text{ }$ — некоторый угол, который называется аргумент комплексного числа (пишут $\text{ }\!\!\varphi\!\!\text{ }=\arg \left( z \right)$).
Любое число $z=a+bi$, отличное от нуля, можно записать с тригонометрической форме. Для этого нужно вычислить модуль и аргумент. Например:
Записать в тригонометрической форме число $z=\sqrt{3}+i$.
Переписываем исходное число в виде $z=\sqrt{3}+1\cdot i$ и считаем модуль:
\[\left| z \right|=\sqrt{{{\left( \sqrt{3} \right)}^{2}}+{{1}^{2}}}=2\]
Выносим модуль за скобки:
\[z=\sqrt{3}+1\cdot i=2\cdot \left( \frac{\sqrt{3}}{2}+\frac{1}{2}\cdot i \right)\]
Вспоминаем тригонометрию, 10-й класс:
\[\frac{\sqrt{3}}{2}=\cos \frac{\text{ }\!\!\pi\!\!\text{ }}{6};\quad \frac{1}{2}=\sin \frac{\text{ }\!\!\pi\!\!\text{ }}{6}\]
Окончательный ответ:
\[z=2\cdot \left( \cos \frac{\text{ }\!\!\pi\!\!\text{ }}{6}+i\cdot \sin \frac{\text{ }\!\!\pi\!\!\text{ }}{6} \right)\]
Понятно, что вместо $\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$ с тем же успехом можно взять аргумент $\frac{13\text{ }\!\!\pi\!\!\text{ }}{6}$. Синус и косинус не поменяется. Главное — выбрать такой аргумент, чтобы в тригонометрической форме не осталось никаких минусов. Все минусы должны уйти внутрь синуса и косинуса. Сравните:
Записать в тригонометрической форме число $z=-1-i$.
Правильно:
\[z=\sqrt{2}\cdot \left( \cos \frac{5\text{ }\!\!\pi\!\!\text{ }}{4}+i\sin \frac{5\text{ }\!\!\pi\!\!\text{ }}{4} \right)\]
Неправильно:
\[\begin{align} & z=-\sqrt{2}\cdot \left( \cos \frac{\text{ }\!\!\pi\!\!\text{ }}{4}+i\sin \frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right) \\ & z=\sqrt{2}\cdot \left( -\cos \frac{\text{ }\!\!\pi\!\!\text{ }}{4}-i\sin \frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right) \\ & z=\sqrt{2}\cdot \left( \cos \frac{3\text{ }\!\!\pi\!\!\text{ }}{4}-i\sin \frac{3\text{ }\!\!\pi\!\!\text{ }}{4} \right) \\ \end{align}\]
Комплексные числа, записанные в тригонометрической форме, очень удобно умножать и делить.
Теорема. Пусть даны два комплексных числа:
\[\begin{align} & {{z}_{1}}=\left| {{z}_{1}} \right|\cdot \left( \cos \alpha +i\sin \alpha \right) \\ & {{z}_{2}}=\left| {{z}_{2}} \right|\cdot \left( \cos \beta +i\sin \beta \right) \\ \end{align}\]
Тогда их произведение равно
\[{{z}_{1}}\cdot {{z}_{2}}=\left| {{z}_{1}} \right|\cdot \left| {{z}_{2}} \right|\cdot \left( \cos \left( \alpha +\beta \right)+i\sin \left( \alpha +\beta \right) \right)\]
А если ещё и $\left| {{z}_{2}} \right|\ne 0$, то их частное равно
\[\frac{{{z}_{1}}}{{{z}_{2}}}=\frac{\left| {{z}_{1}} \right|}{\left| {{z}_{2}} \right|}\cdot \left( \cos \left( \alpha -\beta \right)+i\sin \left( \alpha -\beta \right) \right)\]
Получается, что при умножении комплексных чисел мы просто умножаем их модули, а аргументы складываем. При делении — делим модули и вычитаем аргументы. И всё!
Найти произведение и частное двух комплексных чисел:
\[\begin{align} & {{z}_{1}}=2\cdot \left( \cos \frac{\pi }{3}+i\sin \frac{\pi }{3} \right) \\ & {{z}_{2}}=5\cdot \left( \cos \frac{\pi }{6}+i\sin \frac{\pi }{6} \right) \\ \end{align}\]
Считаем произведение:
\[\begin{align} {{z}_{1}}\cdot {{z}_{2}} & =2\cdot 5\cdot \left( \cos \left( \frac{\pi }{3}+\frac{\pi }{6} \right)+i\sin \left( \frac{\pi }{3}+\frac{\pi }{6} \right) \right)= \\ & =10\cdot \left( \cos \frac{\pi }{2}+i\sin \frac{\pi }{2} \right) \\ \end{align}\]
Считаем частное:
\[\begin{align} \frac{{{z}_{1}}}{{{z}_{2}}} & =\frac{2}{5}\cdot \left( \cos \left( \frac{\pi }{3}-\frac{\pi }{6} \right)+i\sin \left( \frac{\pi }{3}-\frac{\pi }{6} \right) \right)= \\ & =0,4\cdot \left( \cos \frac{\pi }{6}+i\sin \frac{\pi }{6} \right) \\ \end{align}\]
По сравнению со стандартной (алгебраической) формой записи комплексных чисел экономия сил и времени налицо.:)
Пусть дано комплексное число в тригонометрической форме:
\[z=\left| z \right|\cdot \left( \cos \text{ }\!\!\varphi\!\!\text{ }+i\sin \text{ }\!\!\varphi\!\!\text{ } \right)\]
Возведём его в квадрат, умножив на само себя:
\[\begin{align} {{z}^{2}} & =z\cdot z = \\ & =\left| z \right|\left| z \right|\cdot \left( \cos \left( \text{ }\!\!\varphi\!\!\text{ + }\!\!\varphi\!\!\text{ } \right)+i\sin \left( \text{ }\!\!\varphi\!\!\text{ + }\!\!\varphi\!\!\text{ } \right) \right)= \\ & ={{\left| z \right|}^{2}}\cdot \left( \cos 2\text{ }\!\!\varphi\!\!\text{ }+i\sin 2\text{ }\!\!\varphi\!\!\text{ } \right) \\ \end{align}\]
Затем возведём в куб, умножив на себя ещё раз:
\[{{z}^{3}}={{\left| z \right|}^{3}}\cdot \left( \cos 3\varphi +i\sin 3\varphi \right)\]
Несложно догадаться, что будет дальше — при возведении в степень $n$. Это называется формула Муавра.
Формула Муавра. При возведении всякого комплексного числа
\[z=\left| z \right|\cdot \left( \cos \varphi +i\sin \varphi \right)\]
в степень $n\in \mathbb{N}$ получим
\[{{z}^{n}}={{\left| z \right|}^{n}}\cdot \left( \cos \left( n\varphi \right)+i\sin \left( n\varphi \right) \right)\]
Простая формула, которая ускоряет вычисления раз в десять! И кстати: эта формула работает при любом $n\in \mathbb{R}$, а не только натуральном. Но об этом позже. Сейчас примеры:
Вычислить:
\[{{\left( \sqrt{3}-i \right)}^{16}}\]
Представим первое число в тригонометрической форме:
\[\begin{align} \sqrt{3}-i & = 2\cdot \left( \frac{\sqrt{3}}{2}+i\cdot \left( -\frac{1}{2} \right) \right)= \\ & =2\cdot \left( \cos \left( -\frac{\pi }{6} \right)+i\sin \left( -\frac{\pi }{6} \right) \right) \\ \end{align}\]
По формуле Муавра:
\[\begin{align} & {{\left( 2\cdot \left( \cos \frac{11\pi }{6}+i\sin \frac{11\pi }{6} \right) \right)}^{16}}= \\ & ={{2}^{16}}\cdot \left( \cos \frac{88\pi }{3}+i\sin \frac{88\pi }{3} \right)= \\ & ={{2}^{16}}\cdot \left( \cos \frac{4\pi }{3}+i\sin \frac{4\pi }{3} \right) \\ \end{align}\]
Последним шагом мы воспользовались периодичностью синуса и косинуса, уменьшив аргумент сразу на 28π.
Следующую задачу в разных вариациях любят давать на контрольных работах и экзаменах:
Вычислить:
\[{{\left( \left( -\frac{\sqrt{2}}{2} \right)+\left( -\frac{\sqrt{2}}{2} \right)i \right)}^{2022}}\]
Теперь второе число запишем в комплексной форме:
\[\begin{align} & \left( -\frac{\sqrt{2}}{2} \right)+\left( -\frac{\sqrt{2}}{2} \right)i= \\ & =1\cdot \left( \cos \frac{5\pi }{4}+i\sin \frac{5\pi }{4} \right) \\ \end{align}\]
По формуле Муавра:
\[\begin{align} & {{\left( 1\cdot \left( \cos \frac{5\pi }{4}+i\sin \frac{5\pi }{4} \right) \right)}^{2022}}= \\ & ={{1}^{2022}}\cdot \left( \cos \frac{5055\pi }{2}+i\sin \frac{5055\pi }{2} \right)= \\ & =1\cdot \left( \cos \frac{3\pi }{2}+i\sin \frac{3\pi }{2} \right)=-i \\ \end{align}\]
Вот так всё просто! Следующие два раздела предназначены для углублённого изучения. Для тех, кто хочет действительно разобраться в комплексных числах.
Многие путают местами косинус и синус. Почему комплексная единица стоит именно у синуса? Вспомним, что есть декартова система координат, где точки задаются отступами по осям $x$ и $y$:
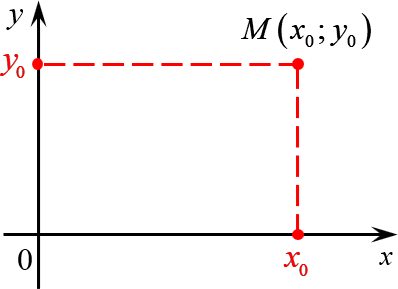
А есть полярная система координат, где точки задаются поворотом на угол $\varphi $ и расстоянием до центра $r$:
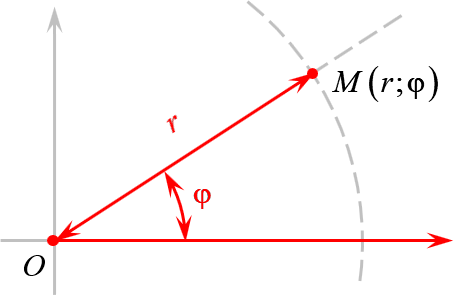
А теперь объединим эти картинки и попробуем перейти из декартовой системы координат в полярную:
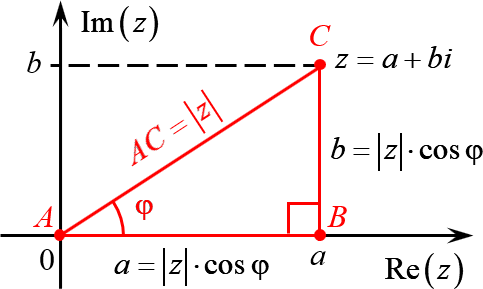
Комплексное число $z=a+bi$ задаёт на плоскости точку $C$, удалённую от начала координат на расстояние
\[AC=\sqrt{{{a}^{2}}+{{b}^{2}}}=\left| z \right|\]
Треугольник $ABC$ — прямоугольный. Пусть $\angle BAC=\varphi $. Тогда:
\[\begin{align} & AB=AC\cdot \cos \varphi =\left| z \right|\cdot \cos \varphi \\ & BC=AC\cdot \sin \varphi =\left| z \right|\cdot \sin \varphi \\ \end{align}\]
С другой стороны, длины катетов $AB$ и $BC$ — это те самые отступы $a$ и $b$, с помощью которых мы задаём комплексное число. Поэтому:
\[\begin{align} a+bi & =\left| z \right|\cos \varphi +i\cdot \left| z \right|\sin \varphi = \\ & =\left| z \right|\left( \cos \varphi +i\sin \varphi \right) \\ \end{align}\]
Итак, мы перешли от пары $\left( a;b \right)$ к паре $\left( \left| z \right|;\varphi \right)$, где $\left| z \right|$ — модуль комплексного числа, $\varphi $ — его аргумент (проще говоря, угол поворота).
Важное замечание. А кто сказал, что такой угол $\varphi $ существует? Возьмём число $z=a+bi$ и вынесем модуль за скобку:
\[\begin{align} z & =a+bi= \\ & =\sqrt{{{a}^{2}}+{{b}^{2}}}\cdot \left( \frac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}}}+i\cdot \frac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right)= \\ & =\left| z \right|\cdot \left( \cos \text{ }\!\!\varphi\!\!\text{ }+i\sin \text{ }\!\!\varphi\!\!\text{ } \right) \\ \end{align}\]
Осталось подобрать такой угол $\varphi $, чтобы выполнялось два равенства:
\[\begin{align} & \frac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}}}=\cos \text{ }\!\!\varphi\!\!\text{ } \\ & \frac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}}}=\sin \text{ }\!\!\varphi\!\!\text{ } \\ \end{align}\]
Такой угол обязательно найдётся, поскольку выполняется основное тригонометрическое тождество:
\[\begin{align} {{\sin }^{2}}\text{ }\!\!\varphi\!\!\text{ } & +{{\cos }^{2}}\text{ }\!\!\varphi\!\!\text{ }= \\ & ={{\left( \frac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right)}^{2}}+{{\left( \frac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right)}^{2}}= \\ & =\frac{{{a}^{2}}}{{{a}^{2}}+{{b}^{2}}}+\frac{{{b}^{2}}}{{{a}^{2}}+{{b}^{2}}}=\frac{{{a}^{2}}+{{b}^{2}}}{{{a}^{2}}+{{b}^{2}}}=1 \\ \end{align}\]
На практике основная трудность заключается именно в поиске подходящего аргумента.
В учебниках пишут много разной дичи, типа вот этой:
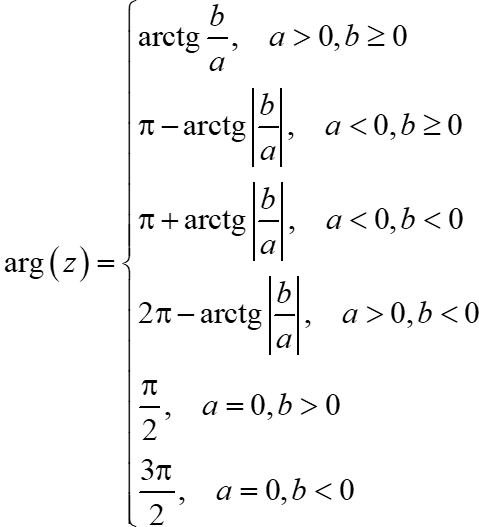
Формула правильная, но пользы от неё — ноль. Запомнить сложно, а применять и вовсе невозможно. Мы пойдём другим путём.
Для начала рассмотрим точки, лежащие осях координат.
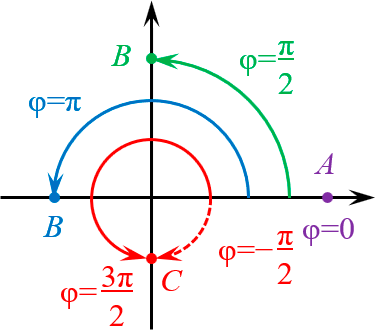
Тут всё очевидно:
А если точки не лежат на осях, то в записи комплексного числа $a+bi$ числа $a\ne 0$ и $b\ne 0$. Рассмотрим вспомогательный угол
\[{{\varphi }_{1}}=\operatorname{arctg}\left| \frac{b}{a} \right|\]
Очевидно, это острый угол:
\[0 \lt \operatorname{arctg}\left| \frac{a}{b} \right| \lt \frac{\pi }{2}\]
Зная знаки чисел $a$ и $b$, мы немедленно определим координатную четверть, в которой располагается искомая точка. И нам останется лишь отложить вспомогательный угол ${{\varphi }_{1}}$ от горизонтальной оси в эту четверть.
В правой полуплоскости мы откладываем от «нулевого» луча:
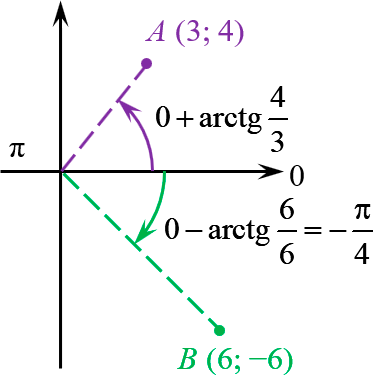
Точка $A\left( 3;4 \right)$ удалена от начала координат на расстояние 5:
\[\begin{align} 3+4i & =5\cdot \left( \cos \varphi +i\sin \varphi \right) \\ \varphi & =\operatorname{arctg}\frac{4}{3} \end{align}\]
Для точки $B\left( 6;-6 \right)$ арктангенс оказался табличным:
\[6-6i=6\sqrt{2}\cdot \left( \cos \left( -\frac{\pi }{4} \right)+i\sin \left( -\frac{\pi }{4} \right) \right)\]
В левой полуплоскости откладываем от луча, соответствующего углу $\pi $:
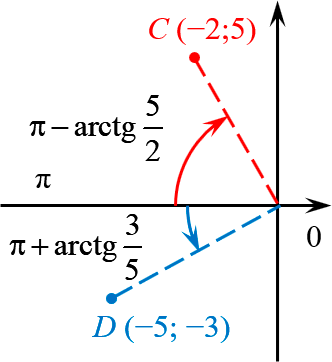
Итого для точки $C\left( -2;5 \right)$ имеем:
\[\begin{align} -2+5i & =\sqrt{29}\cdot \left( \cos \varphi +i\sin \varphi \right) \\ \varphi & =\pi -\operatorname{arctg}\frac{5}{2} \end{align}\]
И, наконец, для точки $D\left( -5;-3 \right)$:
\[\begin{align} -5-3i & =\sqrt{34}\cdot \left( \cos \varphi +i\sin \varphi \right) \\ \varphi & =\pi +\operatorname{arctg}\frac{3}{5} \end{align}\]
Звучит просто, выглядит красиво, работает идеально! Но требует небольшой практики. Пробуйте, тренируйтесь и берите на вооружение.
А в следующем уроке мы научимся извлекать корни из комплексных чисел.:)