Итак, сегодня мы пошагово разберем довольно сложную задачу на смеси и сплавы, которая в итоге сведется к системе из двух уравнений. После просмотра этого видео вы будете щелкать эти задачи как орешки — потому что на самом деле они не такие уж и сложные.:)
Сегодня мы продолжаем рассматривать текстовые задачи из ЕГЭ по математике и на очереди у нас задача про смеси и сплавы. Обычно я решаю такие задачи про смеси и сплавы с помощью таблиц, подобно примерам на движение и производительность труда. Однако недавно с учениками мы опробовали новый, более наглядный способ решения, который оказался быстрее, чем способ решения с помощью таблиц, но самое главное — он оказался таким же правильным и понятным, как и классические приемы. Давайте попробуем.
Задача:
Имеются два сосуда. Первый содержит
Давайте переведем это условие на язык математики. У нас есть сосуд, который содержит
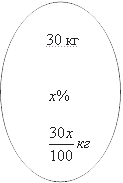
Теперь переходим ко второму сосуду. В нем имеется
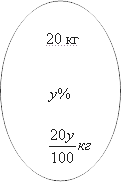
А теперь согласно условию мы смешиваем эти растворы и получаем новый со следующими параметрами. Разумеется, масса новой смеси будет равна сумме масс исходных смесей, т. е. 20+30=5020+30=50. При этом mm чистой кислоты при смешивании также складываются. А это значит что ее масса в новом веществе равна:
30100+20y100
\frac{30}{100}+\frac{20y}{100}
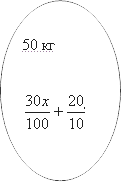
Но с другой стороны, эта же смесь может быть описана следующими цифрами. Ееmm все также составляет
50⋅68100
50\cdot \frac{68}{100}
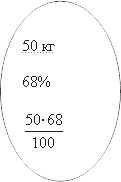
А поскольку в обеих кружках описан один и тот же раствор, мы можем первое выражение приравнять ко второму. Мы получим следующее уравнение:
30x100+20y100=50⋅68100
\frac{30x}{100}+\frac{20y}{100}=\frac{50\cdot \text{68}}{\text{100}}
3x−2y=5⋅68
3x-2y=5\cdot 68
3x+2y=340
3x+2y=340
Итак, мы получили первое уравнение задачи на смеси и сплавы. Возвращаемся к условию задачи про смеси и сплавы и читаем дальше: если же смешать равные массы этих растворов, то получится вещество, содержащее 70% кислоты.
Давайте чертить новые кружки. У нас есть два раствора, но теперь их масса не 30 и
Итак, первая смесь. Ее mm
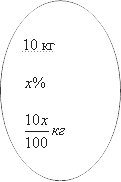
Для второго примера, концентрация которого составляет yy%, mm составит
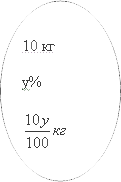
Теперь мы смешиваем их и получаем новый. При этом их массы тоже складываются:
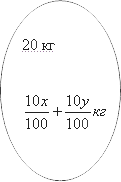
С другой стороны этот же раствор можно описать следующими цифрами: у нас есть
20⋅70
20\cdot 70
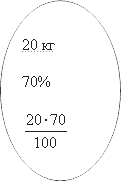
Поскольку данные в двух последних кружках равны, то мы можем записать следующее уравнение:
10x100+10y100=20 ⋅ 70100
\frac{10x}{100}+\frac{10y}{100}=\frac{\text{20 }\!\!\cdot\!\!\text{ 70}}{\text{100}}
x+y=140
x+y=140
Итак, мы получили второе уравнение, которое вместе с первым образует систему:
{3x + 2y = 340x+y=140}
\left\{ \left. \begin{align}& \text{3x }+\text{ 2y }=\text{ 340} \\& \text{x}+\text{y}=\text{140} \\\end{align} \right\} \right.
Сейчас мы и будем ее решать. Давайте сначала выпишем эту систему.
Второе уравнение в нашей системе симметрично относительно переменных xx и yy, т. е. мы можем одинаковыми усилиями выразить и x и y. Так какую же переменную выражать? Для того, чтобы понять, какая из них оптимальная, давайте вернемся обратно к задаче и прочитаем вопрос: сколько килограммов чистого вещества содержится в первом сосуде? Именно первый сосуд. Концентрация, как мы помним, равна xx%. Следовательно, при решении этой системы уравнений задачи на смеси и сплавы нас, в первую очередь, интересует х. А это значит, что именно через xx мы должны выразить все, что у нас есть, в данном случае у. Этот прием используется во всех более-менее сложных задачах на смеси и сплавы.
При решении системы уравнений мы стараемся выразить не ту переменную, которая первой попадется нам на глаза, а ту, от которой нужно избавиться, чтобы получить одно уравнение с одной переменной, решение которой даст нам непосредственно ответ к задаче. Такой переменной у нас является xx, потому что зная xx, мы сразу найдем массу чистого вещества в первом сосуде, что от нас и требуется. А это значит, что через xx мы выражаем все остальное, в данном случае у. Давайте подставим:
{3x+2y=340x+y=140}
\left\{ \left. \begin{align}& \text{3}x+\text{2}y=\text{340} \\& x+y=\text{140} \\\end{align} \right\} \right.
{3x+2(140−x)=340y=140−x}
\left. \left\{ \begin{align}& 3x+2(140-x)=340 \\& y=140-x \\\end{align} \right. \right\}
3x+2(140−x)=340
3x+2(140-x)=340
3x+280−2x=340
3x+280-2x=340
x=60
x=60
Итак, мы нашли концентрацию чистого вещества в первом растворе. Она составляет 60%. Давайте подставим это число в выражение чистой mm, т. е.
30⋅60100=3⋅6=18
30\cdot \frac{60}{100}=3\cdot 6=18
Вот и все, мы получили ответ —
Давайте еще раз быстренько пробежимся по всем ключевым этапам решения этой задачи на смеси и сплавы. В первую очередь необходимо понять, что это за выражения стоять внизу кружочков, которые означают наши растворы. На самом деле все очень просто. Если есть некий раствор массой MM, в котором известно, что xx% этого раствора составляет кислота, то ее MM будет выражаться по формуле:
M⋅x100
M\cdot \frac{x}{100}
Эту формулу легко запомнить, если понять, что M100\frac{M}{100} — это 1% от MM исходного вещества.
Записывая таким образом массы чистой кислоты для каждого из веществ, а также для вещества, которое получается для смешивания, мы легко составим уравнение. Для этого нужно понимать, что при смешивании mm не меняется. Именно поэтому мы складываем $M$ кислоты в исходных веществах и приравниваем их к массе чистой кислоты в исходном веществе.
А дальше все просто. У нас получается да линейных уравнения, которые легко объединяются в систему, а затем решаются. Единственный момент, который возникает при решении таких систем состоит в том, что нужно выбрать самое простое уравнение и выразить их него не ту переменную, которую мы ищем для ответа на вопрос задачи, а как раз таки все остальное. Другими словами мы берем искомую переменную и через нее выражаем все остальные переменные, которые имеются в задаче.
В нашем случае такая переменная всего одна. Мы выражаем у через xx. А дальше мы получаем одно единственное уравнение относительно той самой переменной, которую мы ищем. Следовательно, всю систему вообще можно отбросить. Такое уравнение обычно легко решается.
Самое главное здесь — не забыть, что же конкретно мы ищем. А ищем мы вовсе не концентрацию исходной кислоты в процентах, а именно массу этой кислоты. Т. е. полученное выражение xx нужно еще подставить в выражение для чистой массы. Сделав это, посчитав полученную дробь, мы получим ответ. В нашем случае он составил
В дополнение к видео хотел бы добавить, что по моим наблюдениям все ученики делятся на два типа:
Если вы относитесь ко второму типу учеников, не переживайте: таких людей около 40%, т.е. очень много. На самом деле задачи на движение и на смеси и сплавы имеют примерно одинаковый уровень педагогической сложности, однако при этом требуют разных навыков для быстрого решения. У кого-то эти навыки есть, а у кого-то — нет. Но если немного потренироваться, то оба типа задач окажутся вполне решаемыми.
Вот и все решение. Если немного потренироваться, то задачи на смеси и сплавы окажутся не такими уж и сложными.