В прошлом видеоуроке мы рассматривали решение задач на проценты с помощью пропорций. Тогда по условию задачи нам требовалось найти значение той или иной величины.
В этот раз исходное и конечное значения нам уже даны. Поэтому в задачах будет требоваться найти проценты. Точнее, на сколько процентов изменилась та или иная величина. Давайте попробуем.
Задача. Кроссовки стоили 3200 рублей. После повышения цены они стали стоить 4000 рублей. На сколько процентов была повышена цена на кроссовки?
Итак, решаем через пропорцию. Первый шаг — исходная цена была равна 3200 рублей. Следовательно, 3200 рублей — это 100%.
Кроме того, нам дана конечная цена — 4000 рублей. Это неизвестное количество процентов, поэтому обозначим его за x. Получим следующую конструкцию:
3200 — 100%
4000 — x%
Что ж, условие задачи записано. Составляем пропорцию:
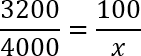
Дробь слева прекрасно сокращается на 100: 3200 : 100 = 32; 4000 : 100 = 40. Кроме того, можно сократить на 4: 32 : 4 = 8; 40 : 4 = 10. Получим следующую пропорцию:
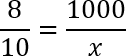
Воспользуемся основным свойством пропорции: произведение крайних членов равно произведению средних. Получаем:
8 · x = 100 · 10;
8x = 1000.
Это обычное линейное уравнение. Отсюда находим x:
x = 1000 : 8 = 125
Итак, мы получили итоговый процент x = 125. Но является ли число 125 решением задачи? Нет, ни в коем случае! Потому что в задачи требуется узнать, на сколько процентов была повышена цена на кроссовки.
На сколько процентов — это значит, что нам нужно найти изменение:
∆ = 125 − 100 = 25
Получили 25% — именно настолько была повышена исходная цена. Это и является ответом: 25.
Переходим ко второй задаче.
Задача. Рубашка стоила 1800 рублей. После снижения цены она стала стоить 1530 рублей. На сколько процентов была снижена цена на рубашку?
Переводим условие на математический язык. Исходная цена 1800 рублей — это 100%. А итоговая цена 1530 рублей — она нам известна, но неизвестно, сколько процентов она составляет от исходной величины. Поэтому обозначим ее за x. Получим следующую конструкцию:
1800 — 100%
1530 — x%
На основе полученной записи составляем пропорцию:
![]()
Давайте для упрощения дальнейших вычислений разделим обе части данного уравнения на 100. Другими словами, у числителя левой и правой дроби мы зачеркнем два нуля. Получим:
![]()
Теперь снова воспользуемся основным свойством пропорции: произведение крайних членов равно произведению средних.
18 · x = 1530 · 1;
18x = 1530.
Осталось найти x:
x = 1530 : 18 = (765 · 2) : (9 · 2) = 765 : 9 = (720 + 45) : 9 = 720 : 9 + 45 : 9 = 80 + 5 = 85
Как видите, мы не стали считать полученное частное уголком, а просто несколько раз сократили нашу дробь. При этом нам потребовалось разложить на множители числитель и
Мы получили, что x = 85. Но, как и в прошлой задаче, это число само по себе не является ответом. Давайте вернемся к нашему условию. Теперь мы знаем, что новая цена, полученная после снижения, составляет 85% от старой. И для того, чтобы найти изменения, нужно из старой цены, т.е. 100%, вычесть новую цену, т.е. 85%. Получим:
∆ = 100 − 85 = 15
Это число и будет ответом: Обратите внимание: именно 15, а ни в коем случае не 85. Вот и все! Задача решена.
Внимательные ученики наверняка спросят: почему в первой задаче мы при нахождении разности вычитали из конечного числа начальное, а во второй задаче поступили в точности до наоборот: из исходных 100% вычли конечные 85%?
Давайте проясним этот момент. Формально, в математике изменением величины всегда называется разность между конечным значением и начальным. Другими словами, во второй задаче у нас должно было получиться не 15, а −15.
Однако этот минус ни в коем случае не должен попасть в ответ, потому что он уже учтен в условии исходной задачи. Там прямо сказано о снижении цены. А снижение цены на 15% — это то же самое, что повышение цены на −15%. Именно поэтому в решении и ответе задачи достаточно написать просто 15 — без всяких минусов.
Все, надеюсь, с этим моментом мы разобрались. На этом наш сегодняшний урок закончен. До новых встреч!