Эта тема является одной из самых ненавистных среди студентов. Хуже, наверное, только определители.
Фишка в том, что само понятие обратного элемента (и я сейчас не только о матрицах) отсылает нас к операции умножения. Даже в школьной программе умножение считается сложной операцией, а уж умножение матриц — вообще отдельная тема, которой у меня посвящён целый параграф и видеоурок.
Сегодня мы не будем вдаваться в подробности матричных вычислений. Просто вспомним: как обозначаются матрицы, как они умножаются и что из этого следует.
Прежде всего договоримся об обозначениях. Матрицей $A$ размера $\left[ m\times n \right]$ называется просто таблица из чисел, в которой ровно $m$ строк и $n$ столбцов:
\[A=\left[ m\times n \right]=\underbrace{\left[ \begin{matrix} {{a}_{11}} & {{a}_{12}} & ... & {{a}_{1n}} \\ {{a}_{21}} & {{a}_{22}} & ... & {{a}_{2n}} \\ ... & ... & ... & ... \\ {{a}_{m1}} & {{a}_{m2}} & ... & {{a}_{mn}} \\\end{matrix} \right]}_{n}\]
Чтобы случайно не перепутать строки и столбцы местами (поверьте, на экзамене можно и единицу с двойкой перепутать — что уж говорить про какие-то там строки), просто взгляните на картинку:
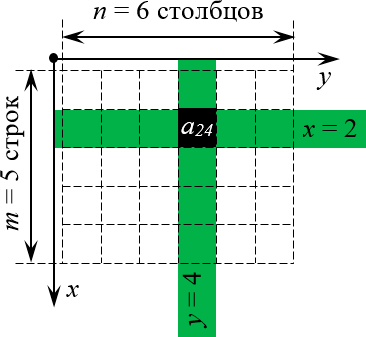
Что происходит? Если разместить стандартную систему координат $OXY$ в левом верхнем углу и направить оси так, чтобы они охватывали всю матрицу, то каждой клетке этой матрицы можно однозначно сопоставить координаты $\left( x;y \right)$ — это и будет номер строки и номер столбца.
Почему система координат размещена именно в левом верхнем углу? Да потому что именно оттуда мы начинаем читать любые тексты. Это очень просто запомнить.
А почему ось $x$ направлена именно вниз, а не вправо? Опять всё просто: возьмите стандартную систему координат (ось $x$ идёт вправо, ось $y$ — вверх) и поверните её так, чтобы она охватывала матрицу. Это поворот на 90 градусов по часовой стрелке — его результат мы и видим на картинке.
В общем, как определять индексы у элементов матрицы, мы разобрались. Теперь давайте разберёмся с умножением.
Определение. Матрицы $A=\left[ m\times n \right]$ и $B=\left[ n\times k \right]$, когда количество столбцов в первой совпадает с количеством строк во второй, называются согласованными.
Именно в таком порядке. Можно сумничать и сказать, мол, матрицы $A$ и $B$ образуют упорядоченную пару $\left( A;B \right)$: если они согласованы в таком порядке, то совершенно необязательно, что $B$ и $A$, т.е. пара $\left( B;A \right)$ — тоже согласована.
Умножать можно только согласованные матрицы.
Определение. Произведение согласованных матриц $A=\left[ m\times n \right]$ и $B=\left[ n\times k \right]$ — это новая матрица $C=\left[ m\times k \right]$, элементы которой ${{c}_{ij}}$ считаются по формуле:
\[{{c}_{ij}}=\sum\limits_{k=1}^{n}{{{a}_{ik}}}\cdot {{b}_{kj}}\]
Другими словами: чтобы получить элемент ${{c}_{ij}}$ матрицы $C=A\cdot B$, нужно взять $i$-строку первой матрицы, $j$-й столбец второй матрицы, а затем попарно перемножить элементы из этой строки и столбца. Результаты сложить.
Да, вот такое суровое определение. Из него сразу следует несколько фактов:
Дистрибутивность умножения пришлось отдельно описывать для левого и правого множителя-суммы как раз из-за некоммутативности операции умножения.
Если всё же получается так, что $A\cdot B=B\cdot A$, такие матрицы называются перестановочными.
Среди всех матриц, которые там на что-то умножаются, есть особые — те, которые при умножении на любую матрицу $A$ снова дают $A$:
Определение. Матрица $E$ называется единичной, если $A\cdot E=A$ или $E\cdot A=A$. В случае с квадратной матрицей $A$ можем записать:
\[A\cdot E=E\cdot A=A\]
Единичная матрица — частый гость при решении матричных уравнений. И вообще частый гость в мире матриц.:)
А ещё из-за этой $E$ кое-кто придумал всю ту дичь, которая будет написана дальше.
Поскольку умножение матриц — весьма трудоёмкая операция (приходится перемножать кучу строчек и столбцов), то понятие обратной матрицы тоже оказывается не самым тривиальным. И требующим некоторых пояснений.
Что ж, пора познать истину.
Определение. Матрица $B$ называется обратной к матрице $A$, если
\[A\cdot B=B\cdot A=E\]
Обратная матрица обозначается через ${{A}^{-1}}$ (не путать со степенью!), поэтому определение можно переписать так:
\[A\cdot {{A}^{-1}}={{A}^{-1}}\cdot A=E\]
Казалось бы, всё предельно просто и ясно. Но при анализе такого определения сразу возникает несколько вопросов:
Насчёт алгоритмов вычисления — об этом мы поговорим чуть позже. Но на остальные вопросы ответим прямо сейчас. Оформим их в виде отдельных утверждений-лемм.
Начнём с того, как в принципе должна выглядеть матрица $A$, чтобы для неё существовала ${{A}^{-1}}$. Сейчас мы убедимся в том, что обе эти матрицы должны быть квадратными, причём одного размера: $\left[ n\times n \right]$.
Лемма 1. Дана матрица $A$ и обратная ей ${{A}^{-1}}$. Тогда обе эти матрицы — квадратные, причём одинакового порядка $n$.
Доказательство. Всё просто. Пусть матрица $A=\left[ m\times n \right]$, ${{A}^{-1}}=\left[ a\times b \right]$. Поскольку произведение $A\cdot {{A}^{-1}}=E$ по определению существует, матрицы $A$ и ${{A}^{-1}}$ согласованы в указанном порядке:
\[\begin{align} & \left[ m\times n \right]\cdot \left[ a\times b \right]=\left[ m\times b \right] \\ & n=a \end{align}\]
Это прямое следствие из алгоритма перемножения матриц: коэффициенты $n$ и $a$ являются «транзитными» и должны быть равны.
Вместе с тем определено и обратное умножение: ${{A}^{-1}}\cdot A=E$, поэтому матрицы ${{A}^{-1}}$ и $A$ тоже согласованы в указанном порядке:
\[\begin{align} & \left[ a\times b \right]\cdot \left[ m\times n \right]=\left[ a\times n \right] \\ & b=m \end{align}\]
Таким образом, без ограничения общности можем считать, что $A=\left[ m\times n \right]$, ${{A}^{-1}}=\left[ n\times m \right]$. Однако согласно определению $A\cdot {{A}^{-1}}={{A}^{-1}}\cdot A$, поэтому размеры матриц строго совпадают:
\[\begin{align} & \left[ m\times n \right]=\left[ n\times m \right] \\ & m=n \end{align}\]
Вот и получается, что все три матрицы — $A$, ${{A}^{-1}}$ и $E$ — являются квадратными размером $\left[ n\times n \right]$. Лемма доказана.
Что ж, уже неплохо. Мы видим, что обратимыми бывают лишь квадратные матрицы. Теперь давайте убедимся, что обратная матрица всегда одна.
Лемма 2. Дана матрица $A$ и обратная ей ${{A}^{-1}}$. Тогда эта обратная матрица — единственная.
Доказательство. Пойдём от противного: пусть у матрицы $A$ есть хотя бы два экземпляра обратных —$B$ и $C$. Тогда, согласно определению, верны следующие равенства:
\[\begin{align} & A\cdot B=B\cdot A=E; \\ & A\cdot C=C\cdot A=E. \\ \end{align}\]
Из леммы 1 мы заключаем, что все четыре матрицы — $A$, $B$, $C$ и $E$ — являются квадратными одинакового порядка: $\left[ n\times n \right]$. Следовательно, определено произведение:
\[B\cdot A\cdot C\]
Поскольку умножение матриц ассоциативно (но не коммутативно!), мы можем записать:
\[\begin{align} & B\cdot A\cdot C=\left( B\cdot A \right)\cdot C=E\cdot C=C; \\ & B\cdot A\cdot C=B\cdot \left( A\cdot C \right)=B\cdot E=B; \\ & B\cdot A\cdot C=C=B\Rightarrow B=C. \\ \end{align}\]
Получили единственно возможный вариант: два экземпляра обратной матрицы равны. Лемма доказана.
Приведённые рассуждения почти дословно повторяют доказательство единственность обратного элемента для всех действительных чисел $b\ne 0$. Единственное существенное дополнение — учёт размерности матриц.
Впрочем, мы до сих пор ничего не знаем о том, всякая ли квадратная матрица является обратимой. Тут нам на помощь приходит определитель — это ключевая характеристика для всех квадратных матриц.
Лемма 3. Дана матрица $A$. Если обратная к ней матрица ${{A}^{-1}}$ существует, то определитель исходной матрицы отличен от нуля:
\[\left| A \right|\ne 0\]
Доказательство. Мы уже знаем, что $A$ и ${{A}^{-1}}$ — квадратные матрицы размера $\left[ n\times n \right]$. Следовательно, для каждой из них можно вычислить определитель: $\left| A \right|$ и $\left| {{A}^{-1}} \right|$. Однако определитель произведения равен произведению определителей:
\[\left| A\cdot B \right|=\left| A \right|\cdot \left| B \right|\Rightarrow \left| A\cdot {{A}^{-1}} \right|=\left| A \right|\cdot \left| {{A}^{-1}} \right|\]
Но согласно определению $A\cdot {{A}^{-1}}=E$, а определитель $E$ всегда равен 1, поэтому
\[\begin{align} & A\cdot {{A}^{-1}}=E; \\ & \left| A\cdot {{A}^{-1}} \right|=\left| E \right|; \\ & \left| A \right|\cdot \left| {{A}^{-1}} \right|=1. \\ \end{align}\]
Произведение двух чисел равно единице только в том случае, когда каждое из этих чисел отлично от нуля:
\[\left| A \right|\ne 0;\quad \left| {{A}^{-1}} \right|\ne 0.\]
Вот и получается, что $\left| A \right|\ne 0$. Лемма доказана.
На самом деле это требование вполне логично. Сейчас мы разберём алгоритм нахождения обратной матрицы — и станет совершенно ясно, почему при нулевом определителе никакой обратной матрицы в принципе не может существовать.
Но для начала сформулируем «вспомогательное» определение:
Определение. Вырожденная матрица — это квадратная матрица размера $\left[ n\times n \right]$, чей определитель равен нулю.
Таким образом, мы можем утверждать, что всякая обратимая матрица является невырожденной.
Сейчас мы рассмотрим универсальный алгоритм нахождения обратных матриц. Вообще, существует два общепринятых алгоритма, и второй мы тоже сегодня рассмотрим.
Тот, который будет рассмотрен сейчас, очень эффективен для матриц размера $\left[ 2\times 2 \right]$ и — частично — размера $\left[ 3\times 3 \right]$. А вот начиная с размера $\left[ 4\times 4 \right]$ его лучше не применять. Почему — сейчас сами всё поймёте.
Готовьтесь. Сейчас будет боль. Нет, не переживайте: к вам не идёт красивая медсестра в юбке, чулках с кружевами и не сделает укол в ягодицу. Всё куда прозаичнее: к вам идут алгебраические дополнения и Её Величество «Союзная Матрица».
Начнём с главного. Пусть имеется квадратная матрица размера $A=\left[ n\times n \right]$, элементы которой именуются ${{a}_{ij}}$. Тогда для каждого такого элемента можно определить алгебраическое дополнение:
Определение. Алгебраическое дополнение ${{A}_{ij}}$ к элементу ${{a}_{ij}}$, стоящего в $i$-й строке и $j$-м столбце матрицы $A=\left[ n\times n \right]$ — это конструкция вида
\[{{A}_{ij}}={{\left( -1 \right)}^{i+j}}\cdot M_{ij}^{*}\]
Где $M_{ij}^{*}$ — определитель матрицы, полученной из исходной $A$ вычёркиванием той самой $i$-й строки и $j$-го столбца.
Ещё раз. Алгебраическое дополнение к элементу матрицы с координатами $\left( i;j \right)$ обозначается как ${{A}_{ij}}$ и считается по схеме:
Саму матрицу $M_{ij}^{*}$ называют дополнительным минором к элементу ${{a}_{ij}}$. И в этом смысле приведённое выше определение алгебраического дополнения является частным случаем более сложного определения — того, что мы рассматривали в уроке про определитель.
Важное замечание. Вообще-то во «взрослой» математике алгебраические дополнения определяются так:
- Берём в квадратной матрице $k$ строчек и $k$ столбцов. На их пересечении получится матрица размера $\left[ k\times k \right]$ — её определитель называется минором порядка $k$ и обозначается ${{M}_{k}}$.
- Затем вычёркиваем эти «избранные» $k$ строчек и $k$ столбцов. Снова получится квадратная матрица — её определитель называется дополнительным минором и обозначается $M_{k}^{*}$.
- Умножаем $M_{k}^{*}$ на ${{\left( -1 \right)}^{t}}$, где $t$ — это (вот сейчас внимание!) сумма номеров всех выбранных строчек и столбцов. Это и будет алгебраическое дополнение.
Взгляните на третий шаг: там вообще-то сумма $2k$ слагаемых! Другое дело, что для $k=1$ мы получим лишь 2 слагаемых — это и будут те самые $i+j$ — «координаты» элемента ${{a}_{ij}}$, для которого мы ищем алгебраическое дополнение.
Таким образом сегодня мы используем слегка упрощённое определение. Но как мы увидим в дальнейшем, его окажется более чем достаточно. Куда важнее следующая штука:
Определение. Союзная матрица $S$ к квадратной матрице $A=\left[ n\times n \right]$ — это новая матрица размера $\left[ n\times n \right]$, которая получается из $A$ заменой ${{a}_{ij}}$ алгебраическими дополнениями ${{A}_{ij}}$:
\[A=\left[ \begin{matrix} {{a}_{11}} & {{a}_{12}} & ... & {{a}_{1n}} \\ {{a}_{21}} & {{a}_{22}} & ... & {{a}_{2n}} \\ ... & ... & ... & ... \\ {{a}_{n1}} & {{a}_{n2}} & ... & {{a}_{nn}} \\\end{matrix} \right]\Rightarrow S=\left[ \begin{matrix} {{A}_{11}} & {{A}_{12}} & ... & {{A}_{1n}} \\ {{A}_{21}} & {{A}_{22}} & ... & {{A}_{2n}} \\ ... & ... & ... & ... \\ {{A}_{n1}} & {{A}_{n2}} & ... & {{A}_{nn}} \\\end{matrix} \right]\]
Первая мысль, возникающая в момент осознания этого определения — «это сколько же придётся всего считать!» Расслабьтесь: считать придётся, но не так уж и много.:)
Что ж, всё это очень мило, но зачем это нужно? А вот зачем.
Вернёмся немного назад. Помните, в Лемме 3 утверждалось, что обратимая матрица $A$ всегда не вырождена (т.е. её определитель отличен от нуля: $\left| A \right|\ne 0$).
Так вот, верно и обратное: если матрица $A$ не вырождена, то она всегда обратима. И даже существует схема поиска ${{A}^{-1}}$. Зацените:
Теорема об обратной матрице. Пусть дана квадратная матрица $A=\left[ n\times n \right]$, причём её определитель отличен от нуля: $\left| A \right|\ne 0$. Тогда обратная матрица ${{A}^{-1}}$ существует и считается по формуле:
\[{{A}^{-1}}=\frac{1}{\left| A \right|}\cdot {{S}^{T}}\]
А теперь — всё то же самое, но разборчивым почерком. Чтобы найти обратную матрицу, нужно:
И всё! Обратная матрица ${{A}^{-1}}$ найдена. Давайте посмотрим на примеры:
Задача. Найдите обратную матрицу:
\[\left[ \begin{matrix} 3 & 1 \\ 5 & 2 \\\end{matrix} \right]\]
Решение. Проверим обратимость. Посчитаем определитель:
\[\left| A \right|=\left| \begin{matrix} 3 & 1 \\ 5 & 2 \\\end{matrix} \right|=3\cdot 2-1\cdot 5=6-5=1\]
Определитель отличен от нуля. Значит, матрица обратима. Составим союзную матрицу:
\[S=\left[ \begin{matrix} {{A}_{11}} & {{A}_{12}} \\ {{A}_{21}} & {{A}_{22}} \\\end{matrix} \right]\]
Посчитаем алгебраические дополнения:
\[\begin{align} & {{A}_{11}}={{\left( -1 \right)}^{1+1}}\cdot \left| 2 \right|=2; \\ & {{A}_{12}}={{\left( -1 \right)}^{1+2}}\cdot \left| 5 \right|=-5; \\ & {{A}_{21}}={{\left( -1 \right)}^{2+1}}\cdot \left| 1 \right|=-1; \\ & {{A}_{22}}={{\left( -1 \right)}^{2+2}}\cdot \left| 3 \right|=3. \\ \end{align}\]
Обратите внимание: определители |2|, |5|, |1| и |3| — это именно определители матриц размера $\left[ 1\times 1 \right]$, а не модули. Т.е. если в определителях стояли отрицательные числа, убирать «минус» не надо.
Итого наша союзная матрица выглядит так:
\[S=\left[ \begin{array}{*{35}{r}}2 & -5 \\ -1 & 3 \\\end{array} \right]\]
Осталось посчитать обратную:
\[{{A}^{-1}}=\frac{1}{\left| A \right|}\cdot {{S}^{T}}=\frac{1}{1}\cdot {{\left[ \begin{array}{*{35}{r}} 2 & -5 \\ -1 & 3 \\\end{array} \right]}^{T}}=\left[ \begin{array}{*{35}{r}} 2 & -1 \\ -5 & 3 \\\end{array} \right]\]
Ну вот и всё. Задача решена.
Ответ. $\left[ \begin{array}{*{35}{r}} 2 & -1 \\ -5 & 3 \\\end{array} \right]$
Задача. Найдите обратную матрицу:
\[\left[ \begin{array}{*{35}{r}} 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end{array} \right]\]
Решение. Опять считаем определитель:
\[\begin{align} & \left| \begin{array}{*{35}{r}} 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end{array} \right|=\begin{matrix} \left( 1\cdot 2\cdot 1+\left( -1 \right)\cdot \left( -1 \right)\cdot 1+2\cdot 0\cdot 0 \right)- \\ -\left( 2\cdot 2\cdot 1+\left( -1 \right)\cdot 0\cdot 1+1\cdot \left( -1 \right)\cdot 0 \right) \\\end{matrix}= \\ & =\left( 2+1+0 \right)-\left( 4+0+0 \right)=-1\ne 0. \\ \end{align}\]
Определитель отличен от нуля — матрица обратима. А вот сейчас будет самая жесть: надо посчитать аж 9 (девять, мать их!) алгебраических дополнений. И каждое из них будет содержать определитель $\left[ 2\times 2 \right]$. Полетели:
\[\begin{matrix} {{A}_{11}}={{\left( -1 \right)}^{1+1}}\cdot \left| \begin{matrix} 2 & -1 \\ 0 & 1 \\\end{matrix} \right|=2; \\ {{A}_{12}}={{\left( -1 \right)}^{1+2}}\cdot \left| \begin{matrix} 0 & -1 \\ 1 & 1 \\\end{matrix} \right|=-1; \\ {{A}_{13}}={{\left( -1 \right)}^{1+3}}\cdot \left| \begin{matrix} 0 & 2 \\ 1 & 0 \\\end{matrix} \right|=-2; \\ ... \\ {{A}_{33}}={{\left( -1 \right)}^{3+3}}\cdot \left| \begin{matrix} 1 & -1 \\ 0 & 2 \\\end{matrix} \right|=2; \\ \end{matrix}\]
Короче, союзная матрица будет выглядеть так:
\[S=\left[ \begin{matrix} 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\end{matrix} \right]\]
Следовательно, обратная матрица будет такой:
\[{{A}^{-1}}=\frac{1}{-1}\cdot \left[ \begin{matrix} 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\end{matrix} \right]=\left[ \begin{array}{*{35}{r}}-2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end{array} \right]\]
Ну и всё. Вот и ответ.
Ответ. $\left[ \begin{array}{*{35}{r}} -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end{array} \right]$
Как видите, в конце каждого примера мы выполняли проверку. В связи с этим важное замечание:
Не ленитесь выполнять проверку. Умножьте исходную матрицу на найденную обратную — должна получиться $E$.
Выполнить эту проверку намного проще и быстрее, чем искать ошибку в дальнейших вычислениях, когда, например, вы решаете матричное уравнение.
Как я и говорил, теорема об обратной матрице прекрасно работает для размеров $\left[ 2\times 2 \right]$ и $\left[ 3\times 3 \right]$ (в последнем случае — уже не так уж и «прекрасно»), а вот для матриц больших размеров начинается прям печаль.
Но не переживайте: есть альтернативный алгоритм, с помощью которого можно невозмутимо найти обратную хоть для матрицы $\left[ 10\times 10 \right]$. Но, как это часто бывает, для рассмотрения этого алгоритма нам потребуется небольшая теоретическая вводная.
Среди всевозможных преобразований матрицы есть несколько особых — их называют элементарными. Таких преобразований ровно три:
Почему эти преобразования называются элементарными (для больших матриц они выглядят не такими уж элементарными) и почему их только три — эти вопросы выходят за рамки сегодняшнего урока. Поэтому не будем вдаваться в подробности.
Важно другое: все эти извращения нам предстоит выполнять над присоединённой матрицей. Да, да: вы не ослышались. Сейчас будет ещё одно определение — последнее в сегодняшнем уроке.
Наверняка в школе вы решали системы уравнений методом сложения. Ну, там, вычесть из одной строки другую, умножить какую-то строку на число — вот это вот всё.
Так вот: сейчас будет всё то же, но уже «по-взрослому». Готовы?
Определение. Пусть дана матрица $A=\left[ n\times n \right]$ и единичная матрица $E$ такого же размера $n$. Тогда присоединённая матрица $\left[ A\left| E \right. \right]$ — это новая матрица размера $\left[ n\times 2n \right]$, которая выглядит так:
\[\left[ A\left| E \right. \right]=\left[ \begin{array}{rrrr|rrrr}{{a}_{11}} & {{a}_{12}} & ... & {{a}_{1n}} & 1 & 0 & ... & 0 \\{{a}_{21}} & {{a}_{22}} & ... & {{a}_{2n}} & 0 & 1 & ... & 0 \\... & ... & ... & ... & ... & ... & ... & ... \\{{a}_{n1}} & {{a}_{n2}} & ... & {{a}_{nn}} & 0 & 0 & ... & 1 \\\end{array} \right]\]
Короче говоря, берём матрицу $A$, справа приписываем к ней единичную матрицу $E$ нужного размера, разделяем их вертикальной чертой для красоты — вот вам и присоединённая.:)
В чём прикол? А вот в чём:
Теорема. Пусть матрица $A$ обратима. Рассмотрим присоединённую матрицу $\left[ A\left| E \right. \right]$. Если с помощью элементарных преобразований строк привести её к виду $\left[ E\left| B \right. \right]$, т.е. путём умножения, вычитания и перестановки строк получить из $A$ матрицу $E$ справа, то полученная слева матрица $B$ — это обратная к $A$:
\[\left[ A\left| E \right. \right]\to \left[ E\left| B \right. \right]\Rightarrow B={{A}^{-1}}\]
Вот так всё просто! Короче говоря, алгоритм нахождения обратной матрицы выглядит так:
Конечно, сказать намного проще, чем сделать. Поэтому давайте рассмотрим парочку примеров: для размеров $\left[ 3\times 3 \right]$ и $\left[ 4\times 4 \right]$.
Задача. Найдите обратную матрицу:
\[\left[ \begin{array}{*{35}{r}} 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\end{array} \right]\]
Решение. Составляем присоединённую матрицу:
\[\left[ \begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\end{array} \right]\]
Поскольку последний столбец исходной матрицы заполнен единицами, вычтем первую строку из остальных:
\[\begin{align} & \left[ \begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\end{array} \right]\begin{matrix} \downarrow \\ -1 \\ -1 \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end{array} \right] \\ \end{align}\]
Больше единиц нет, кроме первой строки. Но её мы не трогаем, иначе в третьем столбце начнут «размножаться» только что убранные единицы.
Зато можем вычесть вторую строку дважды из последней — получим единицу в левом нижнем углу:
\[\begin{align} & \left[ \begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end{array} \right]\begin{matrix} \ \\ \downarrow \\ -2 \\\end{matrix}\to \\ & \left[ \begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end{array} \right] \\ \end{align}\]
Теперь можно вычесть последнюю строку из первой и дважды из второй — таким образом мы «занулим» первый столбец:
\[\begin{align} & \left[ \begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end{array} \right]\begin{matrix} -1 \\ -2 \\ \uparrow \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrr|rrr} 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end{array} \right] \\ \end{align}\]
Умножим вторую строку на −1, а затем вычтем её 6 раз из первой и прибавим 1 раз к последней:
\[\begin{align} & \left[ \begin{array}{rrr|rrr} 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end{array} \right]\begin{matrix} \ \\ \left| \cdot \left( -1 \right) \right. \\ \ \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrr|rrr} 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end{array} \right]\begin{matrix} -6 \\ \updownarrow \\ +1 \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrr|rrr} 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & 0 & 0 & 4 & -7 & 3 \\\end{array} \right] \\ \end{align}\]
Осталось лишь поменять местами строки 1 и 3:
\[\left[ \begin{array}{rrr|rrr} 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & -18 & 32 & -13 \\\end{array} \right]\]
Готово! Справа — искомая обратная матрица.
Ответ. $\left[ \begin{array}{*{35}{r}}4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\\end{array} \right]$
Задача. Найдите обратную матрицу:
\[\left[ \begin{matrix} 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\\end{matrix} \right]\]
Решение. Снова составляем присоединённую:
\[\left[ \begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end{array} \right]\]
Немного позалимаем, попечалимся от того, сколько сейчас придётся считать... и начнём считать. Для начала «обнулим» первый столбец, вычитая строку 1 из строк 2 и 3:
\[\begin{align} & \left[ \begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end{array} \right]\begin{matrix} \downarrow \\ -1 \\ -1 \\ \ \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end{array} \right] \\ \end{align}\]
Наблюдаем слишком много «минусов» в строках 2—4. Умножим все три строки на −1, а затем «выжжем» третий столбец, вычитая строку 3 из остальных:
\[\begin{align} & \left[ \begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end{array} \right]\begin{matrix} \ \\ \left| \cdot \left( -1 \right) \right. \\ \left| \cdot \left( -1 \right) \right. \\ \left| \cdot \left( -1 \right) \right. \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 & 1 & -1 & 0 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \\\end{array} \right]\begin{matrix} -2 \\ -1 \\ \updownarrow \\ -2 \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrrr|rrrr} 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end{array} \right] \\ \end{align}\]
Теперь самое время «поджарить» последний столбец исходной матрицы: вычитаем строку 4 из остальных:
\[\begin{align} & \left[ \begin{array}{rrrr|rrrr} 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end{array} \right]\begin{matrix} +1 \\ -3 \\ -2 \\ \uparrow \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrrr|rrrr} 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end{array} \right] \\ \end{align}\]
Финальный бросок: «выжигаем» второй столбец, вычитая строку 2 из строки 1 и 3:
\[\begin{align} & \left[ \begin{array}{rrrr|rrrr} 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end{array} \right]\begin{matrix} 6 \\ \updownarrow \\ -5 \\ \ \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrrr|rrrr} 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end{array} \right] \\ \end{align}\]
И снова слева единичная матрица, значит справа — обратная.:)
Ответ. $\left[ \begin{matrix} 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & -1 \\\end{matrix} \right]$
Ну вот и всё. Проверку сделайте сами — мне в лом.:)