Сегодня мы продолжаем рассматривать задачи на экстремумы из ЕГЭ по математике. Итак, задача:
Задача B15. Найдите точку максимума на отрезке (0; π/2):
y = (3 − 12x) sin x − 12 cos x + 16
Сразу сделаю небольшое лирическое отступление. Дело в том, что это предпоследний урок из серии уроков, посвященным производным в ЕГЭ по математике. И сразу скажу, что оба эти урока будут посвящены тригонометрии, а точнее, нестандартным задачам на тригонометрию.
Вот и сейчас перед нами довольно-таки нестандартная задача. Хотя, как мы убедимся через пару минут, решается она довольно просто.
Давайте в первую очередь посмотрим, что от нас требуется. А требуется найти точку максимума. Заметьте: не наибольшее или наименьшее значение, а именно точку максимума. Из этого сразу следует, что наши любимые приемы, чтобы как-то подобрать х, как-то выделить красиво значение функции — в данной задаче эти приемы не работают просто потому, что значение функции нас не интересует.
Давайте работать по старинке. Прежде всего, я запишу общий алгоритм решения подобных задач.
Вот и все, что нам нужно знать для решения сегодняшней задачи.
Однако некоторые ученики скажут: «На третьем этапе мы отбираем корни только в тех задачах, где требуется найти значение функции, а не точку максимума или минимума. Зачем выполнять отбор корней?»
Согласен, в большинстве задач на поиск точки экстремума отбирать точки не нужно, однако в нашем случае речь идет о тригонометрических функциях, и, как следствие, уравнение y' = 0 будет иметь бесконечное множество корней. Вы что будете отмечать множество корней?
А еще нужно искать между ними знаки, смотреть, где «плюс» переходить в «минус». Это бред! Поэтому, когда вы видите, что в задаче требуется найти производную тригонометрической функции, просто запомните для себя: мы в любом случае отбираем корни на интервале, независимо от того, требуется ли от нас найти значение функции или просто точку минимума или максимума.
При вычислении точек максимума/минимума тригонометрической функции отбор корней на отрезке не просто желателен — такой отбор становится необходимостью!
Это замечание существенно упрощает задачу, потому что лучше отметить один или два корня и посмотреть знаки вокруг них, чем бегать по всей числовой прямой и выяснять, где стоят плюсы, а где — минусы.
Все, с разъяснениями мы закончили, переходим к решению конкретной задачи.
Итак, первый шаг: нужно найти производную функции:
y' = ((3 − 12x) sin x − 12 cos x + 16)' = ((3 − 12x) · sin x)' − (12 cos x)'
Первое слагаемое у нас представляет собой произведение двух функций, в каждой из которых присутствует элемент х, следовательно, нам нужно посчитать производную произведения. Напомню формулу производной произведения:
(f · g)' = f ' · g + f · g'
Запомните, что производная произведения не равна произведению производных. Считаем:
((3 − 12x) · sin x)' = (3 − 12x)' · sin x + (3 − 12x) · (sin x)' = −12 · sin x + (3 − 12x) · cos x
Все, мы посчитали первое слагаемое. Переходим ко второму:
(12 cos x)' = −12 sin x
Теперь подставляем два значения в нашу исходную формулу. Получим:
y' = −12 · sin x + (3 − 12x) · cos x − (− 12 sin x) = (3 − 12x) cos x
Мы нашли производную и выполнили первый шаг нашего алгоритма. Переходим ко второму шагу:
(3 − 12x) cos x = 0
Произведение равно 0, когда хотя бы один из множителей равен 0. Получаем:
3 − 12x = 0
cos x = 0
Из первого уравнения легко находится х:
x = 3/12 = 1/4
А второе равнение — это обычное тригонометрическое равнение. Мы можем сразу записать ответ:
x = π/2 + πn, n ∈ Z
Прекрасно, второй шаг нашего алгоритма выполнен!
Итак, мы нашли вес корни. Теперь отбираем те корни, которые лежат на интервале (0; π/2).
Пока отложим корти, которые получились из тригонометрического уравнения, потому что это более сложная конструкция, и таких корней бесконечное множество.
Решать будем с помощью тригонометрического круга. Давайте отметим все точки в пределах (0; π/2):
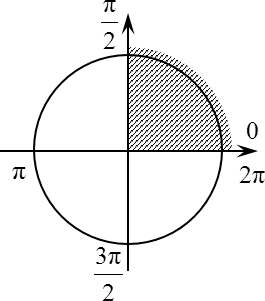
Нижняя точка нас не устраивает, как и не устраивает верхняя точка, потому что они лежат на концах интервала. А сами концы нас не устраивает просто потому, что в исходном условии задачи концы интервала обозначены выколотыми точками, т. е. круглыми скобками. Следовательно, точка π/2 нас тоже не интересует, и поэтому нужно вычеркнуть весь набор корней.
Остается лишь один корень — 1/4. Возникает вопрос: принадлежит ли он интервалу (0; π/2)? Проверяется это очень просто: приравниваем 1/4 с 0 и π/2:
0 ∨ 1/4 ∨ π/2
То, что 1/4 больше, чем 0, а вот с π/2 придется немного повозиться.
1/4 ∨ π/2 > 2 · 3 = 6
0 < 1/4 < π/2
Следовательно, корень 1/4 принадлежит к интересующему нас интервалу (0; π/2). На этом можно было бы закончить решение, потому что мы нашли единственный корень, который нас интересует и который лежит на рассматриваемом интервале и, следовательно, только он может являться ответом.
Можно записать ответ: 1/4 или 0,25.
Однако давайте убедимся, что это действительно точка максимума. Для этого начертим прямую, т. е. перейдем к 4-ому шагу, отметим точку 1/4, а также концы интервала 0 и π/2.
Здесь же отметим знаки. Для этого подставляем любое число в пределах от 0 до 1/4 в изначальную производную. Например, какую-нибудь одну тысячную:
y' (0,001) = (3 − 0, 012) ∙ cos 0,001 > 0
Очевидно, что это число будет больше 0. Кроме того, cos x в пределах промежутка (0; π/2) везде положительный.
Произведение двух положительных чисел является положительным числом. Следовательно, в пределах от 0 до 1/4 знак будет «плюс». А число 1/4 является корнем первой кратности, так как у нас нет никаких квадратов, т. е. при переходе через него знак поменяется:
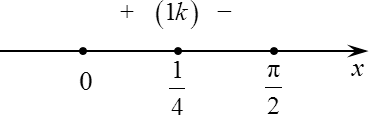
Мы получаем, что в точке x = 1/4 знак производной меняется с «плюса» на «минус». Следовательно, точка x = 1/4 является точкой максимума. Теперь задача точно решена, и мы еще раз убедились, что ответом будет число 0,25.
Итого, несмотря на довольно угрожающий вид функции, все решается просто и быстро. Главное — не забывайте, по какой формуле считается производная произведения, иначе ответ точно получится неправильный.
Кроме того, настоятельно рекомендую вам потренироваться в отборе корней на интервале, иначе вы замучаетесь отмечать бесконечный набор корней на числовой прямой.
В остальном же это стандартная задача B15 на экстремумы, которая решается классическими приемами из математического анализа и вполне доступна среднестатистическому ученику.
Надеюсь, этот урок поможет тем, кто готовится к ЕГЭ по математике. А у меня на сегодня все. С вами был Павел Бердов. До новых встреч!