Этим видео я начинаю длинную серию уроков, посвященную производным. Этот урок состоит из нескольких частей.
В первую очередь, я расскажу вам, что вообще такое производные и как их считать, но не мудреным академическим языком, а так, как я сам это понимаю и как объясняю своим ученикам. Во-вторых, мы рассмотрим простейшее правило для решения задач, в которых будем искать производные суммы, производные разности и производные степенной функции.
Мы рассмотрим более сложные комбинированные примеры, из которых вы, в частности, узнаете, что подобные задачи, содержащие корни и даже дроби, могут быть решены при использовании формулы производной степенной функции. Кроме того, конечно, будет множество задач и примеров решений самого разного уровня сложности.
Вообще, изначально я собирался записать коротенький 5-минутный ролик, но сами видите, что из этого получилось. Поэтому хватит лирики — приступаем к делу.
Итак, начнем издалека. Много лет назад, когда деревья были зеленее, а жизнь была веселее, математики задумались вот над чем: рассмотрим простую функцию, заданную своим графиком, назовем ее $y=f\left( x \right)$. Разумеется, график существует не сам по себе, поэтому нужно провести оси $x$, а также ось $y$. А теперь давайте выберем любую точку на этом графике, абсолютно любую. Абсциссу назовем ${{x}_{1}}$, ордината, как не трудно догадаться, будет $f\left( {{x}_{1}} \right)$.
Рассмотрим на том же графике еще одну точку. Не важно, какую, главное, чтобы она отличалась от первоначальной. У нее, опять же, есть абсцисса, назовем ее ${{x}_{2}}$, а также ордината — $f\left( {{x}_{2}} \right)$.
Итак, мы получили две точки: у них разные абсциссы и, следовательно, разные значения функции, хотя последнее — необязательно. А вот что действительно важно, так это что, что из курса планиметрии нам известно: через две точки можно провести прямую и, причем, только одну. Вот давайте ее и проведем.
А теперь проведем через самую первую из них прямую, параллельную оси абсцисс. Получим прямоугольный треугольник. Давайте его обозначим $ABC$, прямой угол $C$. У этого треугольника возникает одно очень интересное свойство: дело в том, что угол$\alpha $, на самом деле, равен углу, под которым пересекается прямая $AB$ с продолжением оси абсцисс. Судите сами:
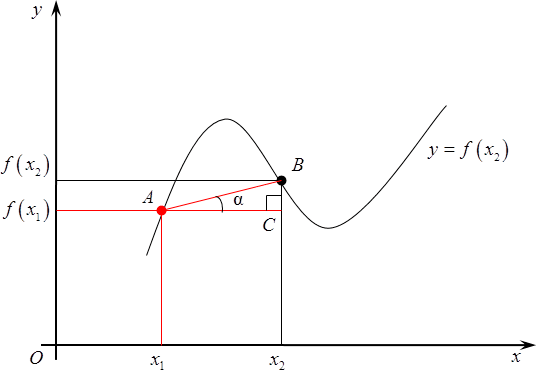
Что мы можем сказать об $\text{ }\!\!\alpha\!\!\text{ }$? Ничего конкретного, разве что в треугольнике $ABC$отношение катета $BC$ к катету $AC$ равно тангенсу этого самого угла. Так и запишем:
\[tg=\frac{BC}{AC}\]
Разумеется, $AC$ в данном случае легко считается:
\[AC={{x}_{2}}-{{x}_{1}}\]
Точно также и $BC$:
\[BC=f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)\]
Другими словами, мы можем записать следующее:
\[\operatorname{tg}\text{ }\!\!\alpha\!\!\text{ }=\frac{f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)}{{{x}_{2}}-{{x}_{1}}}\]
Теперь, когда мы все это выяснили, давайте вернемся к нашему графику и рассмотрим новую точку $B$. Сотрем старые значения и возьмем и возьмем $B$ где-нибудь поближе к ${{x}_{1}}$. Вновь обозначим ее абсциссу за ${{x}_{2}}$, а ординату — $f\left( {{x}_{2}} \right)$.
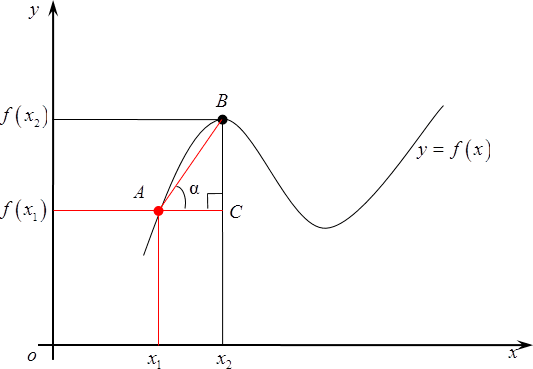
Вновь рассмотрим наш маленький треугольник $ABC$и $\text{ }\!\!\alpha\!\!\text{ }$ внутри него. Совершенно очевидно, что это будет уже совсем другой угол, тангенс будет также другим потому, что длины отрезков $AC$ и $BC$ существенно изменились, а формула для тангенса угла нисколько не поменялась — это по-прежнему соотношение между изменением функции и изменением аргумента.
Наконец, продолжаем двигать $B$ все ближе к изначальной точке $A$, в результате треугольник еще уменьшится, а прямая, содержащая отрезок $AB$, все больше будет походить на касательную к графику функции.
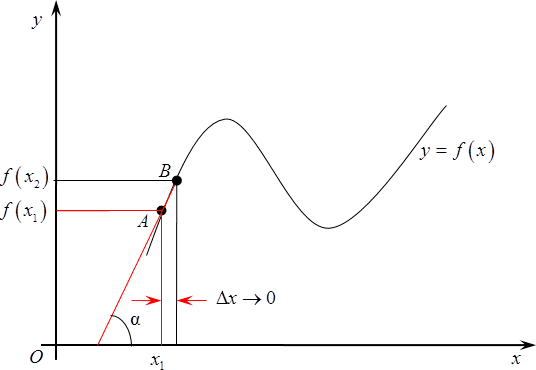
В итоге, если продолжать сближение точек, т. е., уменьшать расстояние до нуля, то прямая $AB$, действительно, превратится в касательную к графику в данной точке, а $\text{ }\!\!\alpha\!\!\text{ }$превратится из обычного элемента треугольника в угол между касательной к графику и положительным направлением оси $Ox$.
И вот тут мы плавно переходим к определению$f$, а именно, производной функции в точке ${{x}_{1}}$ называется тангенс угла $\alpha $ между касательной к графику в точке ${{x}_{1}}$ и положительным направлением оси $Ox$:
\[{f}'\left( {{x}_{1}} \right)=\operatorname{tg}\text{ }\!\!\alpha\!\!\text{ }\]
Возвращаясь к нашему графику, следует отметить, что в качестве ${{x}_{1}}$ можно выбрать любую точку на графике. Например, с тем же успехом мы могли снять штрих в точке, показанной на рисунке.
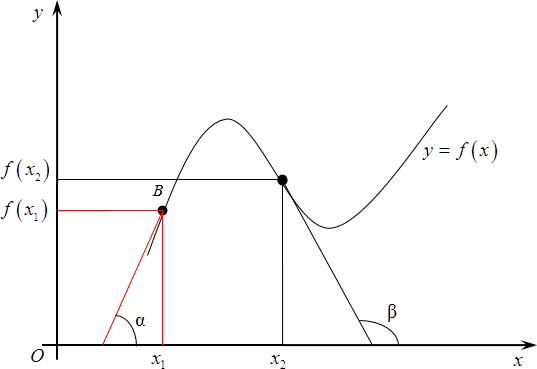
Угол между касательной и положительным направлением оси назовем $\beta $. Соответственно, $f$ в ${{x}_{2}}$ будет равна тангенсу этого угла $\beta $.
\[{f}'\left( {{x}_{2}} \right)=tg\text{ }\!\!\beta\!\!\text{ }\]
В каждой точке графика будет своя касательная, а, следовательно, свое значение функции. В каждом из этих случаев помимо точки, в которой мы ищем производную разности или суммы, или производную степенной функции, необходимо взять другую точку, находящуюся на некотором расстоянии от нее, а затем устремить эту точку к исходной и, разумеется, выяснить, как в процессе такого движения будет меняться тангенс угла наклона.
К сожалению, подобное определение нас совершено не устраивает. Все эти формулы, картинки, углы не дают нам ни малейшего представления о том, как считать реальную производную в реальных задачах. Поэтому давайте немного отвлечемся от формального определения и рассмотрим более действенные формулы и приемы, с помощью которых уже можно решать настоящие задачи.
Начнем с самых простых конструкций, а именно, функций вида $y={{x}^{n}}$, т.е. степенных функций. В этом случае мы можем записать следующее: ${y}'=n\cdot {{x}^{n-1}}$. Другими словами, степень, которая стояла в показателе, показывается в множителе спереди, а сам показатель уменьшается на единицу. Например:
\[\begin{align}& y={{x}^{2}} \\& {y}'=2\cdot {{x}^{2-1}}=2x \\\end{align}\]
А вот другой вариант:
\[\begin{align}& y={{x}^{1}} \\& {y}'={{\left( x \right)}^{\prime }}=1\cdot {{x}^{0}}=1\cdot 1=1 \\& {{\left( x \right)}^{\prime }}=1 \\\end{align}\]
Пользуясь этими простыми правилами, давайте попробуем снять штрих следующих примеров:
\[f\left( x \right)={{x}^{6}}\]
Итак, мы получаем:
\[{{\left( {{x}^{6}} \right)}^{\prime }}=6\cdot {{x}^{5}}=6{{x}^{5}}\]
Теперь решим второе выражение:
\[\begin{align}& f\left( x \right)={{x}^{100}} \\& {{\left( {{x}^{100}} \right)}^{\prime }}=100\cdot {{x}^{99}}=100{{x}^{99}} \\\end{align}\]
Разумеется, это были очень простые задачи. Однако реальные задачи более сложные и они не ограничиваются одними лишь степенями функции.
Итак, правило № 1 – если функция представлена в виде других двух, то производная этой суммы равна сумме производных:
\[{{\left( f+g \right)}^{\prime }}={f}'+{g}'\]
Аналогично, производная разности двух функций равна разности производных:
\[{{\left( f-g \right)}^{\prime }}={f}'-{g}'\]
Пример:
\[{{\left( {{x}^{2}}+x \right)}^{\prime }}={{\left( {{x}^{2}} \right)}^{\prime }}+{{\left( x \right)}^{\prime }}=2x+1\]
Кроме того, есть еще одно важное правило: если перед некоторой $f$ стоит константа $c$, на которую эта функция умножается, то $f$ всей этой конструкции считается так:
\[{{\left( c\cdot f \right)}^{\prime }}=c\cdot {f}'\]
Пример:
\[{{\left( 3{{x}^{3}} \right)}^{\prime }}=3{{\left( {{x}^{3}} \right)}^{\prime }}=3\cdot 3{{x}^{2}}=9{{x}^{2}}\]
Наконец, еще одно очень важное правило: в задачах часто встречается отдельное слагаемое, которое вообще не содержит $x$. Например, мы можем наблюдать это в наших сегодняшних выражениях. Производная константы, т. е., числа, никак не зависящего от $x$, всегда равна нулю, причем совершенно неважно, чему равна константа $c$:
\[{{\left( c \right)}^{\prime }}=0\]
Пример решения:
\[{{\left( 1001 \right)}^{\prime }}={{\left( \frac{1}{1000} \right)}^{\prime }}=0\]
Еще раз ключевые моменты:
Давайте посмотрим, как все это работает на реальных примерах. Итак:
\[y={{x}^{5}}-3{{x}^{2}}+7\]
Записываем:
\[\begin{align}& {{\left( {{x}^{5}}-3{{x}^{2}}+7 \right)}^{\prime }}={{\left( {{x}^{5}} \right)}^{\prime }}-{{\left( 3{{x}^{2}} \right)}^{\prime }}+{7}'= \\& =5{{x}^{4}}-3{{\left( {{x}^{2}} \right)}^{\prime }}+0=5{{x}^{4}}-6x \\\end{align}\]
В этом примере мы видим и производную суммы, и производную разности. Итого, производная равна $5{{x}^{4}}-6x$.
Переходим ко второй функции:
\[f\left( x \right)=3{{x}^{2}}-2x+2\]
Записываем решение:
\[\begin{align}& {{\left( 3{{x}^{2}}-2x+2 \right)}^{\prime }}={{\left( 3{{x}^{2}} \right)}^{\prime }}-{{\left( 2x \right)}^{\prime }}+{2}'= \\& =3{{\left( {{x}^{2}} \right)}^{\prime }}-2{x}'+0=3\cdot 2x-2\cdot 1=6x-2 \\\end{align}\]
Вот мы и нашли ответ.
Переходим к третьей функции — она уже посерьезней:
\[y=2{{x}^{3}}-3{{x}^{2}}+\frac{1}{2}x-5\]
Решаем:
\[\begin{align}& {{\left( 2{{x}^{3}}-3{{x}^{2}}+\frac{1}{2}x-5 \right)}^{\prime }}={{\left( 2{{x}^{3}} \right)}^{\prime }}-{{\left( 3{{x}^{2}} \right)}^{\prime }}+{{\left( \frac{1}{2}x \right)}^{\prime }}-{5}'= \\& =2{{\left( {{x}^{3}} \right)}^{\prime }}-3{{\left( {{x}^{2}} \right)}^{\prime }}+\frac{1}{2}\cdot {x}'=2\cdot 3{{x}^{2}}-3\cdot 2x+\frac{1}{2}\cdot 1=6{{x}^{2}}-6x+\frac{1}{2} \\\end{align}\]
Ответ мы нашли.
Переходим к последнему выражению — самому сложному и самому длинному:
\[y=6{{x}^{7}}-14{{x}^{3}}+4x+5,{{x}_{0}}=-1\]
Итак, считаем:
\[\begin{align}& {{\left( 6{{x}^{7}}-14{{x}^{3}}+4x+5 \right)}^{\prime }}={{\left( 6{{x}^{7}} \right)}^{\prime }}-{{\left( 14{{x}^{3}} \right)}^{\prime }}+{{\left( 4x \right)}^{\prime }}+{5}'= \\& =6\cdot 7\cdot {{x}^{6}}-14\cdot 3{{x}^{2}}+4\cdot 1+0=42{{x}^{6}}-42{{x}^{2}}+4 \\\end{align}\]
Но на этом решение не заканчивается, потому что нас просят не просто снять штрих, а посчитать ее значение в конкретной точке, поэтому подставляем в выражение −1 вместо $x$:
\[{y}'\left( -1 \right)=42\cdot 1-42\cdot 1+4=4\]
Идем далее и переходим к еще более сложным и интересным примерам. Дело в том, что формула решения степенной производной ${{\left( {{x}^{n}} \right)}^{\prime }}=n\cdot {{x}^{n-1}}$ имеет еще более широкую область применения, чем обычно принято считать. С ее помощью можно решать примеры с дробями, корнями и т. д. Именно этим мы сейчас и займемся.
Для начала еще раз запишем формулу, которая поможет нам найти производную степенной функции:
\[{{\left( {{x}^{n}} \right)}^{\prime }}=n\cdot {{x}^{n-1}}\]
А теперь внимание: до сих пор мы рассматривали в качестве $n$ лишь натуральные числа, однако ничего не мешаем рассмотреть дроби и даже отрицательные числа. Например, мы можем записать следующее:
\[\begin{align}& \sqrt{x}={{x}^{\frac{1}{2}}} \\& {{\left( \sqrt{x} \right)}^{\prime }}={{\left( {{x}^{\frac{1}{2}}} \right)}^{\prime }}=\frac{1}{2}\cdot {{x}^{-\frac{1}{2}}}=\frac{1}{2}\cdot \frac{1}{\sqrt{x}}=\frac{1}{2\sqrt{x}} \\\end{align}\]
Ничего сложного, поэтому посмотрим, как эта формула поможет нам при решении более сложных задач. Итак, пример:
\[y=\sqrt{x}+\sqrt[3]{x}+\sqrt[4]{x}\]
Записываем решение:
\[\begin{align}& \left( \sqrt{x}+\sqrt[3]{x}+\sqrt[4]{x} \right)={{\left( \sqrt{x} \right)}^{\prime }}+{{\left( \sqrt[3]{x} \right)}^{\prime }}+{{\left( \sqrt[4]{x} \right)}^{\prime }} \\& {{\left( \sqrt{x} \right)}^{\prime }}=\frac{1}{2\sqrt{x}} \\& {{\left( \sqrt[3]{x} \right)}^{\prime }}={{\left( {{x}^{\frac{1}{3}}} \right)}^{\prime }}=\frac{1}{3}\cdot {{x}^{-\frac{2}{3}}}=\frac{1}{3}\cdot \frac{1}{\sqrt[3]{{{x}^{2}}}} \\& {{\left( \sqrt[4]{x} \right)}^{\prime }}={{\left( {{x}^{\frac{1}{4}}} \right)}^{\prime }}=\frac{1}{4}{{x}^{-\frac{3}{4}}}=\frac{1}{4}\cdot \frac{1}{\sqrt[4]{{{x}^{3}}}} \\\end{align}\]
Возвращаемся к нашему примеру и записываем:
\[{y}'=\frac{1}{2\sqrt{x}}+\frac{1}{3\sqrt[3]{{{x}^{2}}}}+\frac{1}{4\sqrt[4]{{{x}^{3}}}}\]
Вот такое сложное решение.
Переходим ко второму примеру — здесь всего два слагаемых, но каждое из них содержит как классическую степень, так и корни.
\[y={{x}^{3}}\sqrt[3]{{{x}^{2}}}+{{x}^{7}}\sqrt[3]{x}\]
Сейчас мы узнаем, как найти производную степенной функции, которая, кроме того, содержит и корень:
\[\begin{align}& {{\left( {{x}^{3}}\sqrt[3]{{{x}^{2}}}+{{x}^{7}}\sqrt[3]{x} \right)}^{\prime }}={{\left( {{x}^{3}}\cdot \sqrt[3]{{{x}^{2}}} \right)}^{\prime }}={{\left( {{x}^{3}}\cdot {{x}^{\frac{2}{3}}} \right)}^{\prime }}= \\& ={{\left( {{x}^{3+\frac{2}{3}}} \right)}^{\prime }}={{\left( {{x}^{\frac{11}{3}}} \right)}^{\prime }}=\frac{11}{3}\cdot {{x}^{\frac{8}{3}}}=\frac{11}{3}\cdot {{x}^{2\frac{2}{3}}}=\frac{11}{3}\cdot {{x}^{2}}\cdot \sqrt[3]{{{x}^{2}}} \\& {{\left( {{x}^{7}}\cdot \sqrt[3]{x} \right)}^{\prime }}={{\left( {{x}^{7}}\cdot {{x}^{\frac{1}{3}}} \right)}^{\prime }}={{\left( {{x}^{7\frac{1}{3}}} \right)}^{\prime }}=7\frac{1}{3}\cdot {{x}^{6\frac{1}{3}}}=\frac{22}{3}\cdot {{x}^{6}}\cdot \sqrt[3]{x} \\\end{align}\]
Оба слагаемых посчитаны, осталось записать окончательный ответ:
\[{y}'=\frac{11}{3}\cdot {{x}^{2}}\cdot \sqrt[3]{{{x}^{2}}}+\frac{22}{3}\cdot {{x}^{6}}\cdot \sqrt[3]{x}\]
Мы нашли ответ.
Но и на этом возможности формулы для решения производной степенной функции не заканчиваются. Дело в том, что с ее помощью можно считать не только примеры с корнями, но также и с дробями. Это как раз та редкая возможность, которая значительно упрощает решение таких примеров, но при этом зачастую игнорируется не только учениками, но и учителями.
Итак, сейчас мы попытаемся совместить сразу две формулы. С одной стороны, классическая производная степенной функции
\[{{\left( {{x}^{n}} \right)}^{\prime }}=n\cdot {{x}^{n-1}}\]
С другой стороны мы знаем, что выражение вида $\frac{1}{{{x}^{n}}}$ представимо в виде ${{x}^{-n}}$. Следовательно,
\[\left( \frac{1}{{{x}^{n}}} \right)'={{\left( {{x}^{-n}} \right)}^{\prime }}=-n\cdot {{x}^{-n-1}}=-\frac{n}{{{x}^{n+1}}}\]
Пример:
\[{{\left( \frac{1}{x} \right)}^{\prime }}=\left( {{x}^{-1}} \right)=-1\cdot {{x}^{-2}}=-\frac{1}{{{x}^{2}}}\]
Таким образом, производные простых дробей, где в числителе стоит константа, а в знаменателе — степень, также считаются с помощью классической формулы. Посмотрим, как это работает на практике.
Итак, первая функция:
\[f\left( x \right)=\frac{1}{{{x}^{2}}}\]
Считаем:
\[{{\left( \frac{1}{{{x}^{2}}} \right)}^{\prime }}={{\left( {{x}^{-2}} \right)}^{\prime }}=-2\cdot {{x}^{-3}}=-\frac{2}{{{x}^{3}}}\]
Первый пример решен, переходим ко второму:
\[y=\frac{7}{4{{x}^{4}}}-\frac{2}{3{{x}^{3}}}+\frac{5}{2}{{x}^{2}}+2{{x}^{3}}-3{{x}^{4}}\]
Решаем:
\[\begin{align}& {{\left( \frac{7}{4{{x}^{4}}}-\frac{2}{3{{x}^{3}}}+\frac{5}{2}{{x}^{2}}+2{{x}^{3}}-3{{x}^{4}} \right)}^{\prime }}= \\& ={{\left( \frac{7}{4{{x}^{4}}} \right)}^{\prime }}-{{\left( \frac{2}{3{{x}^{3}}} \right)}^{\prime }}+{{\left( 2{{x}^{3}} \right)}^{\prime }}-{{\left( 3{{x}^{4}} \right)}^{\prime }} \\& {{\left( \frac{7}{4{{x}^{4}}} \right)}^{\prime }}=\frac{7}{4}{{\left( \frac{1}{{{x}^{4}}} \right)}^{\prime }}=\frac{7}{4}\cdot {{\left( {{x}^{-4}} \right)}^{\prime }}=\frac{7}{4}\cdot \left( -4 \right)\cdot {{x}^{-5}}=\frac{-7}{{{x}^{5}}} \\& {{\left( \frac{2}{3{{x}^{3}}} \right)}^{\prime }}=\frac{2}{3}\cdot {{\left( \frac{1}{{{x}^{3}}} \right)}^{\prime }}=\frac{2}{3}\cdot {{\left( {{x}^{-3}} \right)}^{\prime }}=\frac{2}{3}\cdot \left( -3 \right)\cdot {{x}^{-4}}=\frac{-2}{{{x}^{4}}} \\& {{\left( \frac{5}{2}{{x}^{2}} \right)}^{\prime }}=\frac{5}{2}\cdot 2x=5x \\& {{\left( 2{{x}^{3}} \right)}^{\prime }}=2\cdot 3{{x}^{2}}=6{{x}^{2}} \\& {{\left( 3{{x}^{4}} \right)}^{\prime }}=3\cdot 4{{x}^{3}}=12{{x}^{3}} \\\end{align}\]...
Теперь собираем все эти слагаемые в единую формулу:
\[{y}'=-\frac{7}{{{x}^{5}}}+\frac{2}{{{x}^{4}}}+5x+6{{x}^{2}}-12{{x}^{3}}\]
Мы получили ответ.
Однако прежде чем двигаться дальше, хотел бы обратить ваше внимание на форму записи самих исходных выражений: в первом выражении мы записали $f\left( x \right)=...$, во втором: $y=...$ Многие ученики теряются, когда видят разные формы записи. Чем отличаются $f\left( x \right)$ и $y$? На самом деле, ничем. Это просто разные записи с одним и тем же смыслом. Просто когда мы говорим $f\left( x \right)$, то речь идет, прежде всего, о функции, а когда речь идет об $y$, то чаще всего подразумевается график функции. В остальном же это одно и то же, т. е., производная в обоих случаях считается одинаково.
В заключение хотелось бы рассмотреть пару сложных комбинированных задач, в которых используется сразу все то, что мы сегодня рассмотрели. В них нас ждут и корни, и дроби, и суммы. Однако сложными эти примеры будут лишь в рамках сегодняшнего видеоурока, потому что по-настоящему сложные функции производных будут ждать вас впереди.
Итак, заключительная часть сегодняшнего видеоурока, состоящая из двух комбинированных задач. Начнем с первой из них:
\[y={{x}^{3}}-\frac{1}{{{x}^{3}}}+\sqrt[3]{x}\]
Считаем:
\[\begin{align}& {{\left( {{x}^{3}}-\frac{1}{{{x}^{3}}}+\sqrt[3]{x} \right)}^{\prime }}={{\left( {{x}^{3}} \right)}^{\prime }}-{{\left( \frac{1}{{{x}^{3}}} \right)}^{\prime }}+\left( \sqrt[3]{x} \right) \\& {{\left( {{x}^{3}} \right)}^{\prime }}=3{{x}^{2}} \\& {{\left( \frac{1}{{{x}^{3}}} \right)}^{\prime }}={{\left( {{x}^{-3}} \right)}^{\prime }}=-3\cdot {{x}^{-4}}=-\frac{3}{{{x}^{4}}} \\& {{\left( \sqrt[3]{x} \right)}^{\prime }}={{\left( {{x}^{\frac{1}{3}}} \right)}^{\prime }}=\frac{1}{3}\cdot \frac{1}{{{x}^{\frac{2}{3}}}}=\frac{1}{3\sqrt[3]{{{x}^{2}}}} \\\end{align}\]
Производная функции равна:
\[{y}'=3{{x}^{2}}-\frac{3}{{{x}^{4}}}+\frac{1}{3\sqrt[3]{{{x}^{2}}}}\]
Первый пример решен. Рассмотрим вторую задачу:
\[y=-\frac{2}{{{x}^{4}}}+\sqrt[4]{x}+\frac{4}{x\sqrt[4]{{{x}^{3}}}}\]
Во втором примере действуем аналогично:
\[{{\left( -\frac{2}{{{x}^{4}}}+\sqrt[4]{x}+\frac{4}{x\sqrt[4]{{{x}^{3}}}} \right)}^{\prime }}={{\left( -\frac{2}{{{x}^{4}}} \right)}^{\prime }}+{{\left( \sqrt[4]{x} \right)}^{\prime }}+{{\left( \frac{4}{x\cdot \sqrt[4]{{{x}^{3}}}} \right)}^{\prime }}\]
Посчитаем каждое слагаемое отдельно:
\[\begin{align}& {{\left( -\frac{2}{{{x}^{4}}} \right)}^{\prime }}=-2\cdot {{\left( {{x}^{-4}} \right)}^{\prime }}=-2\cdot \left( -4 \right)\cdot {{x}^{-5}}=\frac{8}{{{x}^{5}}} \\& {{\left( \sqrt[4]{x} \right)}^{\prime }}={{\left( {{x}^{\frac{1}{4}}} \right)}^{\prime }}=\frac{1}{4}\cdot {{x}^{-\frac{3}{4}}}=\frac{1}{4\cdot {{x}^{\frac{3}{4}}}}=\frac{1}{4\sqrt[4]{{{x}^{3}}}} \\& {{\left( \frac{4}{x\cdot \sqrt[4]{{{x}^{3}}}} \right)}^{\prime }}={{\left( \frac{4}{x\cdot {{x}^{\frac{3}{4}}}} \right)}^{\prime }}={{\left( \frac{4}{{{x}^{1\frac{3}{4}}}} \right)}^{\prime }}=4\cdot {{\left( {{x}^{-1\frac{3}{4}}} \right)}^{\prime }}= \\& =4\cdot \left( -1\frac{3}{4} \right)\cdot {{x}^{-2\frac{3}{4}}}=4\cdot \left( -\frac{7}{4} \right)\cdot \frac{1}{{{x}^{2\frac{3}{4}}}}=\frac{-7}{{{x}^{2}}\cdot {{x}^{\frac{3}{4}}}}=-\frac{7}{{{x}^{2}}\cdot \sqrt[4]{{{x}^{3}}}} \\\end{align}\]
Все слагаемые посчитаны. Теперь возвращаемся к исходной формуле и складываем вместе все три слагаемых. Получаем, что окончательный ответ будет таким:
\[{y}'=\frac{8}{{{x}^{5}}}+\frac{1}{4\sqrt[4]{{{x}^{3}}}}-\frac{7}{{{x}^{2}}\cdot \sqrt[4]{{{x}^{3}}}}\]
И на этом все. Это был первый наш урок. В следующих уроках мы рассмотрим более сложные конструкции, а также выясним, зачем вообще нужны производные.