Сейчас мы узнаем, что такое бесконечно малая функция, какими свойствами она обладает, а также сформулируем и докажем все ключевые теоремы о бесконечно малых. Для понимания материала нужно знать, что такое предел функции в точке.
Содержание урока:
В этом уроке только базовые вещи! Здесь нет сравнения бесконечно малых функций, нет О-символики и нет эквивалентных бесконечно малых. По этим темам будут отдельные уроки — смело переходите к ним после изучения сегодняшнего материала.
Немного теории.
Определение. Функция $y=\alpha \left( x \right)$ называется бесконечно малой при $x\to a$, если её предел при $x\to a$ равен нулю:
\[\lim\limits_{x\to a} \alpha \left( x \right)=0\]
При этом в роли $a$ может выступать как обычное число, так и «бесконечно удалённая точка». Например, $a=+\infty $. Суть от этого никак не поменяется.
В математическом анализе принято обозначать бесконечно малые функции греческими буквами: $\alpha \left( x \right)$, $\beta \left( x \right)$, $\gamma \left( x \right)$ и т.д. Графики таких функций могут быть самыми разнообразными, но при $x\to a$ они обязательно будут стремиться к нулю, т.е. к оси $OX$.
Рассмотрим несколько примеров.
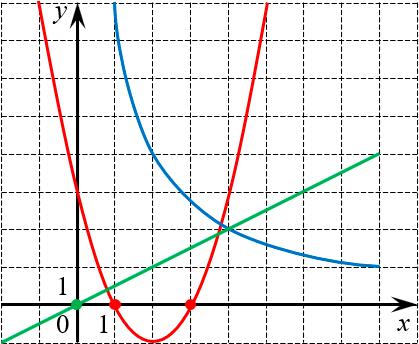
На рисунке изображены три графика:
\[y=\frac{x}{2}\quad y={{x}^{2}}-4x+3\quad y=\frac{8}{x}\]
1. Прямая $y={x}/{2}\;$ пересекает ось $OX$ в начале координат, где $x=0$. И это единственная точка, в которой график приближается к оси $OX$. Во всех остальных точках он либо явно ниже этой оси, либо явно выше. Следовательно, функция $y={x}/{2}\;$ является бесконечно малой при $x\to 0$. Можно записать это так:
\[\alpha \left( x \right)=\frac{x}{2}\to 0\,\quad \left( x\to 0 \right)\]
Или просто вот так:
\[\lim\limits_{x\to 0} \frac{x}{2}=0\]
2. Парабола $y={{x}^{2}}-4x+3$ пересекает ось $OX$ в двух точках: $x=1$ и $x=3$. Следовательно, именно в этих двух точках функция ${{x}^{2}}-4x+3$ является бесконечно малой — и ни в каких других:
\[\begin{align} & \lim\limits_{x\to 1} \left( {{x}^{2}}-4x+3 \right)=0 \\ & \lim\limits_{x\to 3} \left( {{x}^{2}}-4x+3 \right)=0 \\ \end{align}\]
3. Гипербола $y={8}/{x}\;$ вообще не пересекает ось $OX$. Однако по мере роста $x\to +\infty $ гипербола всё ближе «прилегает» к оси $OX$: какой бы отступ вверх мы ни взяли, с какого-то момента ветка гиперболы окажется ближе к оси $OX$, чем этот отступ.
Да это же определение предела функции на бесконечности по Гейне: какой бы отступ $\varepsilon \gt 0$ мы ни взяли, найдётся такое $M \gt 0$, что для всех $x \gt M$ график функции $y={8}/{x}\;$ окажется в пределах этого отступа от нуля:
\[\lim\limits_{x\to +\infty } \frac{8}{x}=0\]
То же самое верно и для $x\to -\infty $. Если вам не понятно, что ещё за $\varepsilon \gt 0$ и $x \gt M$, обязательно повторите определение предела функции по Гейне. А пока я хочу отметить вот что:
Говорить о том, функция является бесконечно малой, можно только в конкретных точках. Таких точек может быть одна, две или даже бесконечно много. Но это всегда конкретные точки.
Просто сказать «бесконечно малая функция» нельзя — такого термина не существует. Нужно обязательно добавить, в какой именно точке мы рассматриваем бесконечно малую.
Часто в задачах просят проверить, что некая функция $\alpha \left( x \right)$ является бесконечно малой при $x\to a$. Сделать это можно как минимум тремя способами:
Свойства пределов мы сегодня разбирать не будем — это отдельный большой урок. Специальные теоремы разберём чуть ниже. А сейчас потренируемся с проверкой по определению.
Пример. Покажите, что функция $y={1}/{{{x}^{3}}}\;$ является бесконечно малой при $x\to +\infty $.
Решение. Чтобы функция была бесконечно малой при $x\to +\infty $, необходимо показать, что
\[\lim\limits_{x\to +\infty } \frac{1}{{{x}^{3}}}=0\]
Следовательно, нужно зафиксировать $\varepsilon \gt 0$ и предъявить такое $M=M\left( \varepsilon \right) \gt 0$, что для всех $x \gt M$ выполнялось условие $\left| 0-{1}/{{{x}^{3}}}\; \right| \lt \varepsilon $. Последнее неравенство легко решается, поскольку при $x\to +\infty $ можно считать $x \gt 0$:
\[\left| \frac{1}{{{x}^{3}}} \right| \lt \varepsilon \Rightarrow {{x}^{3}} \gt \frac{1}{\varepsilon }\Rightarrow x \gt \frac{1}{\sqrt[3]{\varepsilon }}\]
Обозначаем $M={1}/{\sqrt[3]{\varepsilon }}\;$ — это и есть искомое число, которое нужно предъявить.
Пример. Покажите, что функция $y={{\left( x-1 \right)}^{2}}$ является бесконечно малой при $x\to 1$.
Решение. Нужно показать, что
\[\lim\limits_{x\to 1} {{\left( x-1 \right)}^{2}}=0\]
Зафиксируем $\varepsilon \gt 0$ и предъявим такое $\delta =\delta \left( \varepsilon \right) \gt 0$, чтобы для всех $x\in {{\overset{\circ }{\mathop{U}}\,}_{\delta }}\left( 1 \right)$ выполнялось условие $\left| 0-{{\left( x-1 \right)}^{2}} \right| \lt \varepsilon $. Но такое неравенство легко решается:
\[{{\left( x-1 \right)}^{2}} \lt \varepsilon \Rightarrow \left| x-1 \right| \lt \sqrt{\varepsilon }\]
Последнее неравенство буквально означает, что $x$ должен находиться от единицы на расстоянии меньшем, чем $\sqrt{\varepsilon }$. Поэтому обозначаем $\delta =\sqrt{\varepsilon }$ — это и есть искомое $\delta \gt 0$.
Небольшое замечание. Символ ${{\overset{\circ }{\mathop{U}}\,}_{\delta }}\left( 1 \right)$ читается как «проколотая $\delta $-окрестность единицы», т.е. все $x$, отстоящие от единицы менее чем на $\delta $, но не сама единица.
Что такое проколотая окрестность числа и почему мы игнорируем само число — повторите в уроке про окрестности и предельные точки.
Ну хорошо, с определением бесконечно малой функции мы разобрались. Примеры разобрали, проверять бесконечно малые по определению потренировались.
Переходим к свойствам.
Бесконечно малые функции можно складывать, умножать и даже делить (но это не точно — дальше станет понятно, почему). Начнём со сложения.
Теорема. Пусть $\alpha \left( x \right)$ и $\beta \left( x \right)$ — бесконечно малые функции при $x\to a$. Тогда их сумма — тоже бесконечно малая функция.
\[\lim\limits_{x\to a} \left( \alpha \left( x \right)+\beta \left( x \right) \right)=0\]
Доказательство элементарное. Если $\alpha \left( x \right)$ и $\beta \left( x \right)$ — бесконечно малые функции, то
\[\lim\limits_{x\to a} \alpha \left( x \right)=0;\quad \lim\limits_{x\to a} \beta \left( x \right)=0\]
Следовательно, для всякого $\varepsilon \gt 0$ найдётся такое $\delta =\delta \left( \varepsilon \right) \gt 0$, что при \[x\in {{\overset{\circ }{\mathop{U}}\,}_{\delta }}\left( a \right)\] выполнены условия:
\[\left| \alpha \left( x \right)-0 \right| \lt \frac{\varepsilon }{2};\quad \left| \beta \left( x \right)-0 \right| \lt \frac{\varepsilon }{2}\]
Но тогда
\[\left| \alpha \left( x \right)+\beta \left( x \right)-0 \right|\le \left| \alpha \left( x \right) \right|+\left| \beta \left( x \right) \right| \lt \frac{\varepsilon }{2}+\frac{\varepsilon }{2}=\varepsilon \]
\[\begin{align} \left| \alpha \left( x \right)+\beta \left( x \right)-0 \right| & \le \left| \alpha \left( x \right) \right|+\left| \beta \left( x \right) \right| \lt \\ & \lt \frac{\varepsilon }{2}+\frac{\varepsilon }{2}=\varepsilon \\ \end{align}\]
Следовательно, предел суммы действительно равен нулю, поэтому $\alpha \left( x \right)+\beta \left( x \right)$ — бесконечно малая функция.
Теорема доказана. Но её можно обобщить для любой конечной суммы бесконечно малых функций.
Теорема. Пусть ${{\alpha }_{1}}\left( x \right)$,${{\alpha }_{2}}\left( x \right)$, ..., ${{\alpha }_{n}}\left( x \right)$ — $n$ бесконечно малых функции при $x\to a$. Тогда их сумма — тоже бесконечно малая функция:
\[\lim\limits_{x\to a} \sum\limits_{k=1}^{n}{{{\alpha }_{k}}\left( x \right)}=0\]
Доказательство дословно повторяет доказательство предыдущей теоремы. Разница лишь в том, что по фиксированному $\varepsilon \gt 0$ мы будем искать такое $\delta =\delta \left( \varepsilon \right) \gt 0$, чтобы при $x\in {{\overset{\circ }{\mathop{U}}\,}_{\delta }}\left( a \right)$ выполнялись неравенства
\[\left| {{\alpha }_{k}}\left( x \right)-0 \right| \lt \frac{\varepsilon }{n}\quad k\in \left\{ 1;2;\ldots ;n \right\}\]
И сумма будет ограничена:
\[\left| \sum\limits_{k=1}^{n}{{{\alpha }_{k}}\left( x \right)}-0 \right|\le \sum\limits_{k=1}^{n}{\left| {{\alpha }_{k}}\left( x \right) \right|} \lt \sum\limits_{k=1}^{n}{\frac{\varepsilon }{n}}=n\cdot \frac{\varepsilon }{n}=\varepsilon \]
\[\begin{align} \left| \sum\limits_{k=1}^{n}{{{\alpha }_{k}}\left( x \right)}-0 \right| & \le \sum\limits_{k=1}^{n}{\left| {{\alpha }_{k}}\left( x \right) \right|} \lt \\ & \lt \sum\limits_{k=1}^{n}{\frac{\varepsilon }{n}}=n\cdot \frac{\varepsilon }{n}=\varepsilon \\ \end{align}\]
Готово. Снова для заданного $\varepsilon \gt 0$ снова нашли проколотую $\delta $-окрестность точки $x=a$, в которой значения суммы отличаются от нуля не более чем на $\varepsilon $. Теорема доказана.
Сейчас будет две теоремы. Сначала сформулируем и докажем вполне очевидную: умножение бесконечно малых функций при $x\to a$ даёт новую бесконечно малую функция при $x\to a$.
Теорема. Пусть $\alpha \left( x \right)$ и $\beta \left( x \right)$ — бесконечно малые функции при $x\to a$. Тогда их произведение $\alpha \left( x \right)\beta \left( x \right)$ — тоже бесконечно малая функция при $x\to a$, т.е.
\[\lim\limits_{x\to a} \alpha \left( x \right)\beta \left( x \right)=0\]
Доказательство. Зафиксируем $\varepsilon \gt 0$ и найдём $\delta =\delta \left( \varepsilon \right) \gt 0$ такое, чтобы $\left| \alpha \left( x \right)\beta \left( x \right)-0 \right| \lt \varepsilon $. Для этого рассмотрим некое ${{\varepsilon }_{1}}=\min \left( \varepsilon ;1 \right)$ — это либо всё то же самое $\varepsilon $, если оно меньше единицы, либо сама единица. Из чего заключаем, что ${{\varepsilon }_{1}}\le \varepsilon $ и ${{\varepsilon }_{1}}\le 1$. Далее имеем:
\[\lim\limits_{x\to a} \alpha \left( x \right)=\lim\limits_{x\to a} \beta \left( x \right)=0\]
Значит, обязательно найдётся такое $\delta =\delta \left( {{\varepsilon }_{1}} \right) \gt 0$, что для всех $x\in {{\overset{\circ }{\mathop{U}}\,}_{\delta }}\left( a \right)$
\[\begin{align} \left| \alpha \left( x \right)-0 \right| & \lt {{\varepsilon }_{1}}\le 1 \\ \left| \beta \left( x \right)-0 \right| & \lt {{\varepsilon }_{1}}\le 1 \\ \end{align}\]
Но тогда
\[\left| \alpha \left( x \right)\cdot \beta \left( x \right) \right|=\left| \alpha \left( x \right) \right|\cdot \left| \beta \left( x \right) \right| \lt {{\varepsilon }_{1}}\cdot {{\varepsilon }_{1}}\le 1\cdot {{\varepsilon }_{1}}={{\varepsilon }_{1}}\le \varepsilon \]
\[\begin{align} \left| \alpha \left( x \right)\cdot \beta \left( x \right) \right| & =\left| \alpha \left( x \right) \right|\cdot \left| \beta \left( x \right) \right| \lt \\ & \lt {{\varepsilon }_{1}}\cdot {{\varepsilon }_{1}}\le 1\cdot {{\varepsilon }_{1}}= \\ & ={{\varepsilon }_{1}}\le \varepsilon \\ \end{align}\]
Следовательно, при найденном $\delta \gt 0$ в указанной проколотой окрестности $x\in {{\overset{\circ }{\mathop{U}}\,}_{\delta }}\left( a \right)$выполняется условие $\left| \alpha \left( x \right)\beta \left( x \right)-0 \right| \lt \varepsilon $. Теорема доказана.
Но это и так было понятно.
Гораздо интереснее другое: если умножить бесконечно малую функцию при $x\to a$ на некую функцию $f\left( x \right)$, ограниченную в окрестности точки $x=a$, мы вновь получим бесконечно малую.
Теорема. Пусть $\alpha \left( x \right)$ — бесконечно малая функция при $x\to a$. Пусть также в некоторой окрестности точки $x=a$ функция $f\left( x \right)$ ограничена: $\left| f\left( x \right) \right| \lt M$. Тогда функция $\alpha \left( x \right)\cdot f\left( x \right)$ — бесконечно малая при $x\to a$, т.е.
\[\lim\limits_{x\to a} \alpha \left( x \right)\cdot f\left( x \right)=0\]
Доказательство. Поскольку $\alpha \left( x \right)$ — бесконечно малая функция, а функция $f\left( x \right)$ ограничена$\left| f\left( x \right) \right| \lt M$, для любого $\varepsilon \gt 0$ найдётся такое $\delta =\delta \left( \varepsilon \right) \gt 0$, что в проколотой окрестности \[x\in {{\overset{\circ }{\mathop{U}}\,}_{\delta }}\left( a \right)\] выполняется неравенство
\[\left| \alpha \left( x \right)-0 \right| \lt \frac{\varepsilon }{M}\]
Но тогда для функции $\alpha \left( x \right)\cdot f\left( x \right)$ имеем:
\[\left| \alpha \left( x \right)\cdot f\left( x \right)-0 \right|=\left| \alpha \left( x \right)\cdot f\left( x \right) \right|=\left| a\left( x \right) \right|\cdot \left| f\left( x \right) \right| \lt \frac{\varepsilon }{M}\cdot M=\varepsilon \]
\[\begin{align} \left| \alpha \left( x \right)\cdot f\left( x \right)-0 \right| & =\left| \alpha \left( x \right)\cdot f\left( x \right) \right|= \\ & =\left| a\left( x \right) \right|\cdot \left| f\left( x \right) \right| \lt \\ & \lt \frac{\varepsilon }{M}\cdot M=\varepsilon \\ \end{align}\]
Следовательно, предел $\alpha \left( x \right)\cdot f\left( x \right)$ равен нулю:
\[\lim\limits_{x\to a} \alpha \left( x \right)\cdot f\left( x \right)=0\]
А это и означает, что перед нами бесконечно малая функция. Теорема доказана.
Если со сложением и умножением всё более-менее понятно, то вот с делением начинаются проблемы. Рассмотрим две функции:
\[\alpha \left( x \right)=3{{x}^{2}}\quad \beta \left( x \right)={{x}^{4}}\]
Понятно, что обе они являются бесконечно малыми при $x\to 0$:
\[\begin{align} & \lim\limits_{x\to 0} \alpha \left( x \right)=\lim\limits_{x\to 0} 3{{x}^{2}}=0 \\ & \lim\limits_{x\to 0} \beta \left( x \right)=\lim\limits_{x\to 0} {{x}^{4}}=0 \\ \end{align}\]
Что будет, если мы попробуем разделить их друг на друга? При делении ${\beta \left( x \right)}/{\alpha \left( x \right)}\;$ всё хорошо — мы вновь получим бесконечно малую:
\[\lim\limits_{x\to 0} \frac{\beta \left( x \right)}{\alpha \left( x \right)}=\lim\limits_{x\to 0} \frac{{{x}^{4}}}{3{{x}^{2}}}=\lim\limits_{x\to 0} \frac{{{x}^{2}}}{3}=0\]
Но при делении ${\alpha \left( x \right)}/{\beta \left( x \right)}\;$ получим проблему — предел не существует:
\[\lim\limits_{x\to 0} \frac{\alpha \left( x \right)}{\beta \left( x \right)}=\lim\limits_{x\to 0} \frac{3{{x}^{2}}}{{{x}^{4}}}=\lim\limits_{x\to 0} \frac{3}{{{x}^{4}}}=\infty \]
Получается, что при $x\to 0$ функция $\beta \left( x \right)$ устремляется к нулю намного быстрее функции $\alpha \left( x \right)$. Настолько быстро, что даже деление на другую бесконечно малую не смогло остановить этого устремления.:)
Получается, что бесконечно малые функции могут стремиться к нулю с разными скоростями? Да, именно так. Более того: эти скорости можно отслеживать и сравнивать. Можно создать бесконечно малую с нужной скоростью стремления к нулю и делать ещё много чего опасного и интересного.
Но для этого нам нужно взять на вооружение несколько дополнительных приёмов и определений. Всем этим мы и займёмся на следующем уроке.:)