В сегодняшнем уроке мы продолжаем изучать задачи B2 на проценты. В этот раз разберем так называемые задачи комбинированного типа, где расчет процента соседствует с округлением в меньшую или большую сторону в зависимости от условия задачи.
Итак первая задача:
Задача 1. Магазин закупает тарелки по оптовой цене 70 рублей за штуку и продает с наценкой 40%. Какое наибольшее число таких тарелок можно купить в этом магазине на 500 рублей?
Как решать такую задачу? В первую очередь надо понять, что решение будет разбито на 2 этапа:
Итак, поехали! Первый шаг — выясняем стоимость тарелки с учетом наценки. Для этого воспользуемся стандартной формулой простых процентов. А именно:
Теорема о простых процентах. Пусть нам известна исходная величина x, процент изменения k и итоговая величина y. Тогда итоговая величина y выражается через исходную по формуле:
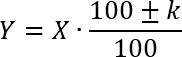
Плюс или минус перед коэффициентом k ставится в зависимости от того, увеличивается рассматриваемая величина или уменьшается.
Очевидно, что в нашем случае величина x будет увеличиваться, поэтому при k будет стоять плюс. Подставляем:
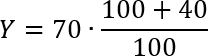
Это обычное уравнение. Выполняем сложение в числителе. Множитель 70 тоже заносим в числитель. Получаем:
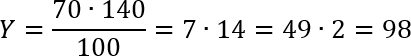
Как видите, все очень легко сокращается и вычисляется. Вот, мы нашли стоимость тарелки с учетом наценки в магазине. Второй шаг — надо узнать: сколько таких тарелок мы купим за 500 рублей. Для этого разделим:
n =
Тут даже не надо ничего придумывать. Думаю, что это очевидно: получится пять целых и что-то там после запятой. Однако нас совершенно не должны интересовать числа после запятой, потому что в задаче требуется найти наибольшее количество таких тарелок. Следовательно, округляем наше число в меньшую сторону и получаем просто
Итак, на 500 рублей мы можем купить 5 тарелок. Причем каждая тарелка в магазине будет стоить 98 рублей, т.е. включать в себя наценку. Все, задача решена! Идем дальше.
Задача 2. Пара носков стоит 160 рублей. Какое наибольшее число таких пар носков можно будет купить на 1000 рублей во время распродажи, когда скидка составляет 20%?
Ну, первым шагом опять же найдем: сколько стоит пара носков с учетом распродажи, т.е. скидки 20%. Для этого снова запишем формулу простого процента:
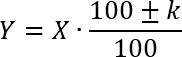
Поскольку в задаче речь идет о скидке, то число k в числителе этой формулы будет стоять с минусом. При этом в качестве x выступает исходная величина, т.е. стоимость носко
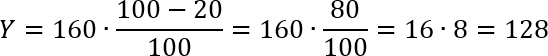
Как видите, все очень просто считается. Достаточно внести множитель 160 в числитель, а затем сократить полученную конструкцию со знаменателем. В результате дробь исчезает, поскольку в знаменателе получается единица. Итого
Вторым шагом находим собственно ответ к задаче, который от нас и требуется. Сколько носков по цене 128 рублей за пару мы можем купить, если у нас в распоряжении только 1000 рублей? Просто разделим 1000 на 128:
n =
Осталось разделить 125 на 16. Можно сделать это уголком, а можно немножко схитрить и записать это действие следующим образом:
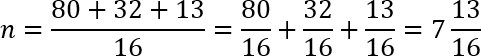
Поясню, откуда взялись числа 80 и 32. Дело в том, что число 125 не делится нацело на
Поэтому мы составляем такое разбиение, чтобы максимально сократить дробь. Далее, как следует из записи, мы разбиваем нашу большую дробь на сумму маленьких дробей, считаем их отдельно и вновь складываем. Получаем, что на 1000 рублей мы можем купить чуть меньше 8 носков.
Теперь возвращаемся к вопросу задачи, который звучит следующим образом: какое наибольшее число таких пар носков можно будет купить? Следовательно, округляем наш предположительный ответ в меньшую сторону и получаем просто
Все, задача решена. Надеюсь, этот урок поможет тем, кто готовится к ЕГЭ по математике. А у меня на этом все! С вами был Павел Бердов. До новых встреч!:)