Чаще всего для решения задач B13, в которых речь идет о многогранниках (именно многогранниках, а не телах вращения!) необходимо применять теорему Пифагора. Сегодняшняя задача наглядно демонстрирует этот факт.
Задача B13. Диагональ AC основания правильной четырехугольной пирамиды SABCD равна 12. Высота пирамиды SH равна 8. Найдите длину бокового ребра SD.
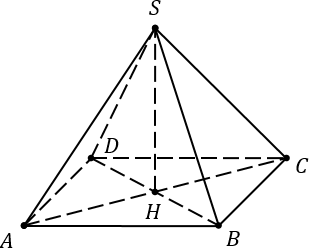
Как можно заметить из видео, задача решается элементарно — достаточно выбрать прямоугольный треугольник и записать для него теорему Пифагора. А затем, разумеется, решить полученное уравнение. Но в том-то и фишка, что многие ученики не могут выбрать нужный треугольник, поэтому рекомендация здесь следующая: ищите треугольник, содержащий сразу две стороны, указанные в условии задачи.