Правила комбинаторики в задаче B6

29 декабря 2011

Решая задачи по теории вероятностей, мы постоянно используем одну и ту же формулу, которая одновременно является классическим определением вероятности:

где k — число благоприятных исходов, n — общее число исходов (см. «Тест по теории вероятностей»).

И эта формула прекрасно работает до тех пор, пока задачи были легкими, а числа, стоящие в числителе и знаменателе — очевидными.

Однако последние пробные экзамены показали, что в настоящем ЕГЭ по математике могут встречаться значительно более сложные конструкции. Отыскание значений n и k становится проблематичным. В таком случае на помощь приходит комбинаторика. Ее законы работают там, где искомые значения не выводятся непосредственно из текста задачи.

В сегодняшнем уроке не будет строгих формулировок и длинных теорем — они слишком сложны и, к тому же, совершенно бесполезны для решения настоящих задач B6. Вместо этого мы рассмотрим простые правила и разберем конкретные задачи, которые действительно встречаются на ЕГЭ. Итак, поехали!

Число сочетаний и факториалы

Пусть имеется n объектов (карандашей, конфет, бутылок водки — чего угодно), из которых требуется выбрать ровно k различных объектов. Тогда количество вариантов такого выбора называется числом сочетаний из n элементов по k. Это число обозначается C_n^k и считается по специальной формуле.

Обозначение:

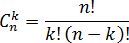
Выражение n! читается как «эн-факториал» и обозначает произведение всех натуральных чисел от 1 до n включительно: n! = 1 · 2 · 3 · ... · n.

Кроме того, в математике по определению считают, что 0! = 1 — подобный бред редко, но все же встречается в задачах по теории вероятностей.

Что дает нам эта формула? На самом деле, без нее не решается практически ни одна серьезная задача.

К сожалению, в школе совершенно не умеют работать с факториалами. Кроме того, в формуле числа сочетаний очень легко запутаться: где стоит и что обозначает число n, а где — k. Поэтому для начала просто запомните: меньшее число всегда стоит сверху — точно так же, как и в формуле определения вероятности (вероятность никогда не бывает больше единицы).

Для лучшего понимания разберем несколько простейших комбинаторных задач:

Задача. У бармена есть 6 сортов зеленого чая. Для проведения чайной церемонии требуется подать зеленый чай ровно 3 различных сортов. Сколькими способами бармен может выполнить заказ?

Тут все просто: есть n = 6 сортов, из которых надо выбрать k = 3 сорта. Число сочетаний можно найти по формуле:

Задача. В группе из 20 студентов надо выбрать 2 представителей для выступления на конференции. Сколькими способами можно это сделать?

Опять же, всего у нас есть n = 20 студентов, а выбрать надо k = 2 студента. Находим число сочетаний:

Обратите внимание: красным цветом отмечены множители, входящие в разные факториалы. Эти множители можно безболезненно сократить и тем самым значительно уменьшить общий объем вычислений.

Задача. На склад завезли 17 серверов с различными дефектами, которые стоят в 2 раза дешевле нормальных серверов. Директор купил в школу 14 таких серверов, а сэкономленные деньги своровал и купил дочке шубу из меха соболя за 200 000 рублей. Сколькими способами директор может выбрать бракованные серверы?

В задаче довольно много лишних данных, которые могут сбить с толку. Наиболее важные факты: всего есть n = 17 серверов, а директору надо k = 14 серверов. Считаем число сочетаний:

Красным цветом снова обозначены множители, которые сокращаются. Итого, получилось 680 комбинаций. В общем, директору есть из чего выбрать.

Как видите, число сочетаний из n по k считается достаточно просто. Проблема в том, что многие школьники никогда не работали с факториалами. Для них это новый и незнакомый математический объект, и для его освоения требуется некоторая тренировка.

Хорошая новость состоит в том, что во многих задачах формулы C_n^k оказывается вполне достаточно для нахождения ответа. Но есть и плохая новость: в тех редких случаях, когда нужны дополнительные правила, решение задачи резко усложняется. Эти правила мы сейчас и рассмотрим.

Закон умножения

Закон умножения в комбинаторике: число сочетаний (способов, комбинаций) в независимых наборах умножается.

Другими словами, пусть имеется A способов выполнить одно действие и B способов выполнить другое действие. Путь также эти действия независимы, т.е. никак не связаны между собой. Тогда можно найти число способов выполнить первое и второе действие по формуле: C = A · B.

Задача. У Пети есть 4 монеты по 1 рублю и 2 монеты по 10 рублей. Петя, не глядя, достал из кармана 1 монету номиналом 1 рубль и еще 1 монету номиналом 10 рублей, чтобы купить сигарету за 11 рублей у бабули в подземном переходе. Сколькими способами он может выбрать эти монеты?

Итак, сначала Петя достает k = 1 монету из n = 4 имеющихся монет номиналом 1 рубль. Число способов сделать это равно C₄¹ = ... = 4.

Затем Петя снова лезет в карман и достает k = 1 монету из n = 2 имеющихся монет номиналом 10 рублей. Здесь число сочетаний равно C₂¹ = ... = 2.

Поскольку эти действия независимы, общее число вариантов равно C = 4 · 2 = 8.

Задача. В корзине лежат 8 белых шаров и 12 черных. Сколькими способами можно достать из этой корзины 2 белых шара и 2 черных?

Всего в корзине n = 8 белых шаров, из которых надо выбрать k = 2 шара. Это можно сделать C₈² = ... = 28 различными способами.

Кроме того, в корзине имеется n = 12 черных шаров, из которых надо выбрать опять же k = 2 шара. Число способов сделать это равно C₁₂² = ... = 66.

Поскольку выбор белого шара и выбор черного — события независимые, общее число комбинаций считается по закону умножения: C = 28 · 66 = 1848. Как видим, вариантов может быть довольно много.

Закон умножения показывает, сколькими способами можно выполнить сложное действие, которое состоит из двух и более простых — при условии, что все они независимы.

Именно этой формулы многим не хватило для решения задачи B6 на пробном ЕГЭ по математике. Разумеется, существуют и другие методы решения, в которых комбинаторика не используется — и мы обязательно рассмотрим их ближе к настоящему экзамену. Однако ни один из них не сравнится по надежности и лаконичности с теми приемами, которые мы сейчас изучаем.

Закон сложения

Если закон умножения оперирует «изолированными» событиями, которые не зависят друг от друга, то в законе сложения все наоборот. Здесь рассматриваются взаимоисключающие события, которые никогда не случаются одновременно.

Например, «Петя вынул из кармана 1 монету» и «Петя не вынул из кармана ни одной монеты» — это взаимоисключающие события, поскольку вынуть одну монету и при этом не вынуть ни одной невозможно.

Аналогично, события «Выбранный наугад шар — белый» и «Выбранный наугад шар — черный» также являются взаимоисключающими.

Закон сложения в комбинаторике: если два взаимоисключающих действия можно выполнить A и B способами соответственно, то эти события можно объединить. При этом возникнет новое событие, которое можно выполнить X = A + B способами.

Другими словами, при объединении взаимоисключающих действий (событий, вариантов) число их комбинаций складывается.

Можно сказать, что закон сложения — это логическое «ИЛИ» в комбинаторике, когда нас устраивает любой из взаимоисключающих вариантов. И наоборот, закон умножения — это логическое «И», при котором нас интересует одновременное выполнение и первого, и второго действия.

Задача. В корзине лежат 9 черных шаров и 7 красных. Мальчик достает 2 шара одинакового цвета. Сколькими способами он может это сделать?

Если шары одинакового цвета, то вариантов немного: оба они либо черные, либо красные. Очевидно, что эти варианты — взаимоисключающие.

В первом случае мальчику предстоит выбирать k = 2 черных шара из n = 9 имеющихся. Число способов сделать это равно C₉² = ... = 36.

Аналогично, во втором случае выбираем k = 2 красных шара из n = 7 возможных. Число способов равно C₇² = ... = 21.

Осталось найти общее количество способов. Поскольку варианты с черными и красными шарами — взаимоисключающие, по закону сложения имеем: X = 36 + 21 = 57.

Задача. В ларьке продаются 15 роз и 18 тюльпанов. Ученик 9-го класса хочет купить 3 цветка для своей одноклассницы, причем все цветы должны быть одинаковыми. Сколькими способами он может составить такой букет?

По условию, все цветы должны быть одинаковыми. Значит, будем покупать либо 3 розы, либо 3 тюльпана. В любом случае, k = 3.

В случае с розами придется выбирать из n = 15 вариантов, поэтому число сочетаний равно C₁₅³ = ... = 455. Для тюльпанов же n = 18, а число сочетаний — C₁₈³ = ... = 816.

Поскольку розы и тюльпаны — это взаимоисключающие варианты, работаем по закону сложения. Получаем общее число вариантов X = 455 + 816 = 1271. Это и есть ответ.

Дополнительные условия и ограничения

Очень часто в тексте задачи присутствуют дополнительные условия, накладывающие существенные ограничения на интересующие нас сочетания. Сравните два предложения:

Имеется набор из 5 ручек разных цветов. Сколькими способами можно выбрать 3 ручки для обводки чертежа?
Имеется набор из 5 ручек разных цветов. Сколькими способами можно выбрать 3 ручки для обводки чертежа, если среди них обязательно должен быть красный цвет?

Чувствуете разницу? В первом случае мы вправе брать любые цвета, какие нам нравятся — дополнительных ограничений нет. Во втором случае все сложнее, поскольку мы обязаны выбрать ручку красного цвета (предполагается, что она есть в исходном наборе).

Очевидно, что любые ограничения резко сокращают итоговое количество вариантов. Ну и как в этом случае найти число сочетаний? Просто запомните следующее правило:

Пусть имеется набор из n элементов, среди которых надо выбрать k элементов. При введении дополнительных ограничений числа n и k уменьшаются на одинаковую величину.

Другими словами, если из 5 ручек надо выбрать 3, при этом одна из них должна быть красной, то выбирать придется из n = 5 − 1 = 4 элементов по k = 3 − 1 = 2 элемента. Таким образом, вместо C₅³ надо считать C₄².

Теперь посмотрим, как это правило работает на конкретных примерах:

Задача. В группе из 20 студентов, среди которых 2 отличника, надо выбрать 4 человека для участия в конференции. Сколькими способами можно выбрать этих четверых, если отличники обязательно должны попасть на конференцию?

Итак, есть группа из n = 20 студентов. Но выбрать надо лишь k = 4 из них. Если бы не было дополнительных ограничений, то количество вариантов равнялось числу сочетаний C₂₀⁴.

Однако нам поставили дополнительное условие: 2 отличника должны быть среди этих четырех. Таким образом, согласно приведенному выше правилу, мы уменьшаем числа n и k на 2. Имеем:

Задача. У Пети в кармане есть 8 монет, из которых 6 монет по рублю и 2 монеты по 10 рублей. Петя перекладывает какие-то три монеты в другой карман. Сколькими способами Петя может это сделать, если известно, что обе монеты по 10 рублей оказались в другом кармане?

Итак, есть n = 8 монет. Петя перекладывает k = 3 монеты, из которых 2 — десятирублевые. Получается, что из 3 монет, которые будут переложены, 2 уже зафиксированы, поэтому числа n и k надо уменьшить на 2. Имеем:

В обоих примерах я намеренно пропустил детали работы с факториалами — попробуйте выполнить все расчеты самостоятельно. Разумеется, для этих задач существуют и другие способы решения. Например, с помощью закона умножения. В любом случае, ответ будет один и тот же.

В заключение отмечу, что в первой задаче мы получили 153 варианта — это намного меньше, чем исходные C₂₀⁴ = ... = 4845 вариантов. Аналогично, 3 монеты из 8 можно переложить C₈³ = ... = 56 способами, что значительно больше 6 способов, которые мы получили в последней задаче.

Эти примеры наглядно демонстрируют, что введение любых ограничений значительно сокращает нашу «свободу выбора».

Смотрите также: