Это первый урок из серии видеоуроков, посвященных задачам B13. Перед нами стандартная задача, которую часто дают на пробниках и контрольных работах. Однако решать ее мы будем весьма нестандартным методом.:)
Задача B13. Дан многогранник, изображенный на рисунке. Все двугранные углы прямые. Найдите, насколько расстояние между вершинами A и C2 отличается от квадрата расстояния между вершинами E и G1. В ответ запишите положительное число.

Для решения любых таких задач нам потребуется обобщенная теорема Пифагора. Давайте отмотаем время назад и вспомним, что такое обычная теорема Пифагора. У нас есть прямоугольный треугольник с катетами a , b и гипотенузой c :

В этом случае квадрат гипотенузы равен сумме квадратов катетов:
c 2 = a 2 + b 2
Но все это рассматривается лишь на плоскости, потому что треугольник — это плоская фигура. Однако та же самая формула работает и в пространстве.
Теорема Пифагора в пространстве. Рассмотрим прямоугольный параллелепипед, или, просто говоря, кирпич. Такой параллелепипед однозначно задается своими сторонами a , b и c . Кроме того, у него есть главная диагональ. Эта диагональ соединяет наиболее удаленные точки параллелепипеда. Разумеется, если параллелепипед прямоугольный, то таких диагоналей сразу несколько, при этом все они будут равны и будут считаться по одной и той же формуле.
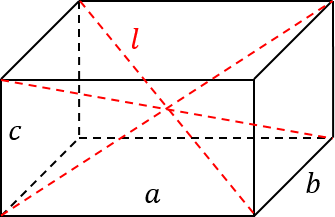
Диагональ обозначим буквой l . В этом случае можно записать формулу:
l 2 = a 2 + b 2 + c 2
Возможно, кто-то сейчас спросит: а какое отношение диагональ, тем более, в параллелепипеде имеет к нашему прямоугольному треугольнику со сторонами a , b и c ? Отношение, на самом деле, самое прямое. Давайте достроим наш треугольник до прямоугольника, и получим, что гипотенуза c является диагональю на прямоугольнике.
Таким образом, перед нами, по сути, аналог теоремы Пифагора для трехмерного пространства. Давайте немножко перепишем ее:
![]()
Внимательные ученики наверняка заметят, что эта формула очень похожа на формулу расстояния в трехмерном пространстве между точками a и b . Разумеется, при условии, что точка A лежала бы в начале координат, а точка B имела координаты, равные длинам сторон нашего параллелепипеда:
A
= (0; 0; 0);
B
= (
a
,
b
,
c
).
Однако ничего удивительного в этом нет, потому что длина диагонали l — это как раз и есть расстояние между наиболее удаленными точками параллелепипеда.
Но хватит теории, давайте перейдем непосредственно к нашей задаче. Итак, в первую очередь нужно найти расстояние от точки A до точки C 2. И вот для того, чтобы найти это расстояние, сейчас мы воспользуемся замечательным приемом, который называется обход точек.
Метод обхода точек заключается в следующем:
Разумеется, последовательность осей может быть любой, решение и ответ от этого не изменится. И двигаться из одной точки в другую тоже можно по-разному. Например, можно идти к точке B , затем к точке C , затем вверх до точки B 2 и, наконец, двигаться вдаль — и мы попадем в точку C 2:
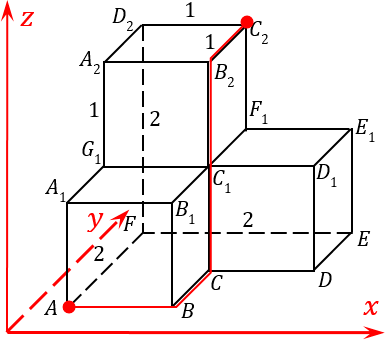
Давайте разметим, полученный нами путь:
А теперь, когда мы отметили каждое звено нашей ломанной, соединяющие точки A и C 2, выпишем, сколько шагов мы получили вдоль каждой координатной оси с учетом знаков:
Теперь возвращается к нашей обобщенной теореме Пифагора и замечаем, что оси x , y и z — это, по сути, a , b и c , т. е. длины сторон параллелепипеда. Следовательно, мы можем посчитать длину диагонали этого параллелепипеда:
![]()
Вот и все! Мы получили расстояние от точки A до C 2, согласно рисунку нашего многогранника.
Однако внимательные ученики спросят: а что будет, если мы пойдем по другому пути? Ведь от точки A до точки C 2 можно идти и другим путем: сначала вверх до точки A 1, затем вглубь до точки G 1, затем вверх до точки A 2, затем снова в глубину до точки D 2, и, наконец вправо до точки C 2:
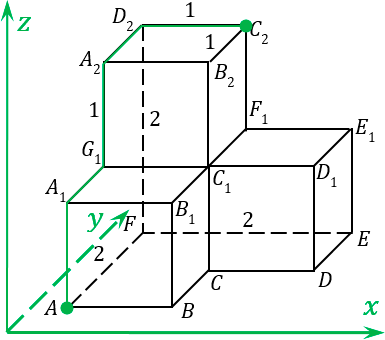
Получили совсем другой маршрут, и возникает логичный вопрос: не будет длина на этом маршруте иметь совсем другое значение координат x , y и z , и, соответственно, другое значение l ? Давайте проверим.
Размечаем наш второй маршрут:
Выписываем полученные смещения:
Итого выражение для диагонали l получилось в точности тем же самым:
![]()
Таким образом, мы убедились, что итоговое значение величины l , т. е. расстояние между точками A и C 2 не зависит от того, каким маршрутом мы будем идти из одной точки в другую. Следовательно, при решении реальных задач вы вправе выбрать любой маршрут, который будет удобен именно вам. И вообще, тот факт, что расстояние между двумя точками не зависит от того, как это расстояние мерить, на самом деле вполне логичен. Мы же занимаемся математикой, а не гаданием на кофейной гуще. Поэтому, по какому бы пути мы не пошли, ответ получится одним и тем же.
Расстояние между двумя точками в пространстве не зависит от того, как мы это расстояние считаем. Если все расчеты выполнены правильно, ответ получится одним и тем же.
Возвращаемся к нашему заданию и переходим ко второй его части. Нужно найти расстояние между точкой E и точкой G 1. Опять предлагаю воспользоваться методом обхода точек. Начнем путь от точки E , будем двигаться к точке D , потом из точки D в точку D 1, и потом от D 1 напрямую в точку G 1:
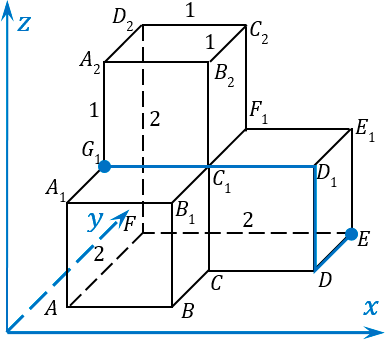
Размечаем нашу ломанную:
Давайте запишем, что у нас получилось:
По каждой из осей зафиксировано лишь одно смещение, ничего складывать, как в предыдущих случаях, не надо. Просто находим длину отрезка, соединяющего точки E и G 1. Давайте назовем этот отрезок l 2. Его длина равна:
![]()
Вспоминаем, что от нас требуется найти в условии задачи. А от нас требуется квадрат расстояния между этими вершинами. Следовательно, нам нужна величина:
l 2 2 = 6
При произведении в квадрат корень исчезает.
Внимательно читайте условие задачи. Недостаточно просто найти длину отрезка или значение переменной — нужно предъявить именно ту величину, которую у нас спрашивают.
Осталось найти ту самую разницу, которую от нас требуют найти в условии задачи. Назовем ее ∆:
∆ = 6 − 3 = 3
Вот мы и нашли ответ — он равен 3.
Еще раз — ключевая идея решения всей этой задачи. Она состоит в том, чтобы прямо на рисунке начертить путь из одной искомой точки в другую и посмотреть: вдоль каких координатных осей выполняется смещение и насколько. Затем мы выписываем эти смещения и считаем общее расстояние по обобщенной теореме Пифагора.
При этом возникает замечательный эффект: итоговое расстояние, которое мы считаем, не зависит от того, какой маршрут обхода мы выберем. В любом случае, как бы мы ни шли из одной точки в другую, расстояние получится одним и тем же. Разумеется, при условии, что все вычисления будут выполнены верно.
Аналогичным образом мы считаем второе расстояние. Пусть вас совершенно не смущает, что тут получаются отрицательные координаты, потому что при возведении в квадрат минусы сжигаются. Наконец, остается сосчитать ту самую разницу, которую требуется найти в условии задачи. Тут вообще все очень просто, и никаких дополнительных пояснений не требуется.
Итак, мы решили задачу B13 мы будем методом обхода точек. Давайте еще раз посмотрим, из каких шагов состояло наше решение:
Но что будет, если выбрать другой маршрут? Не случится ли так, что при этом возникнут другие суммарные смещения и, следовательно, другое расстояние? Спешу вас обрадовать: суммарные смещения и расстояние между точками не зависит от выбранного маршрута. Мы убедились в этом лично, когда рассмотрели альтернативный маршрут обхода.
В общем, чертите путь так, как вам удобно — ответ всегда будет одним и тем же. В этом и состоит прелесть метода обхода точек.