Продолжаем разбираться с углами в пространстве. Сегодня мы разберем более сложную задачу B13 на угол между прямой и плоскостью, однако и она решается буквально в пару строчек.
Задача B13. Боковое ребро правильной треугольной пирамиды равно 25 и наклонено к плоскости основания под углом 30°. Найдите высоту пирамиды.
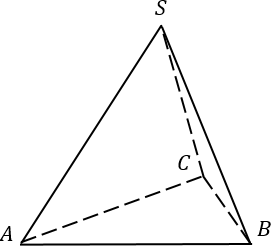
В общем, основная сложность этой задачи — правильно определить точку на плоскости ABC, в которую попадает высота пирамиды. Для справки: высота правильно пирамиды всегда проходит через точку пересечения высот основания.
И именно в этом состоит сложность данной задачи B13 для некоторых учеников: искать надо именно точку пересечения высот, а не диагоналей. Тем более что речь идет о треугольной пирамиде, а в треугольнике нет никаких диагоналей.:)