Сегодня мы рассмотрим очередной тип задач 6 — на этот раз с окружностью. Многие ученики не любят их и считают сложными. И совершенно напрасно, поскольку такие задачи решаются элементарно, если знать некоторые теоремы. Или не решаются вообще, если их не знать.
Прежде чем говорить об основных свойствах, позвольте напомнить определение:
Вписанный угол — тот, у которого вершина лежит на самой окружности, а стороны высекают на этой окружности хорду.
Центральный угол — это любой угол с вершиной в центре окружности. Его стороны тоже пересекают эту окружность и высекают на ней хорду.
Итак, понятия вписанного и центрального угла неразрывно связаны с окружностью и хордами внутри нее. А теперь — основное утверждение:
Теорема. Центральный угол всегда в два раза больше вписанного, опирающегося на ту же самую дугу.
Несмотря на простоту утверждения, существует целый класс задач 6, которые решаются с помощью него — и никак иначе.
Задача. Найдите острый вписанный угол, опирающийся на хорду, равную радиусу окружности.
Пусть AB — рассматриваемая хорда, O — центр окружности. Дополнительное построение: OA и OB — радиусы окружности. Получим:
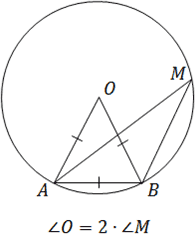
Рассмотрим треугольник ABO. В нем AB = OA = OB — все стороны равны радиусу окружности. Поэтому треугольник ABO — равносторонний, и все углы в нем по 60°.
Пусть M — вершина вписанного угла. Поскольку углы O и M опираются на одну и ту же дугу AB, вписанный угол M в 2 раза меньше центрального угла O. Имеем:
M = O : 2 = 60 : 2 = 30
Задача. Центральный угол на 36° больше вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол.
Введем обозначения:
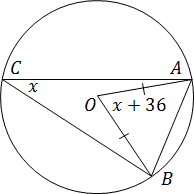
Поскольку мы ищем вписанный угол ACB, обозначим его ACB = x. Тогда центральный угол AOB равен x + 36. С другой стороны, центральный угол в 2 раза больше вписанного. Имеем:
AOB = 2 · ACB;
x + 36 = 2 · x;
x = 36.
Вот мы и нашли вписанный угол AOB — он равен 36°.
Прочитав подзаголовок, знающие читатели, наверное, сейчас скажут: «Фу!» И действительно, сравнивать окружность с углом не совсем корректно. Чтобы понять, о чем речь, взгляните на классическую тригонометрическую окружность:
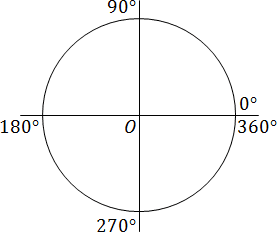
К чему эта картинка? А к тому, что полный оборот — это угол в 360 градусов. И если разделить его, скажем, на 20 равных частей, то размер каждой из них будет 360 : 20 = 18 градусов. Именно это и требуется для решения задачи B8.
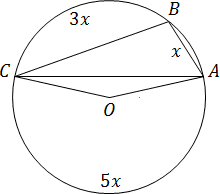
Точки A, B и C лежат на окружности и делят ее на три дуги, градусные меры которых относятся
как 1 : 3 : 5. Найдите больший угол треугольника ABC.
Для начала найдем градусную меру каждой дуги. Пусть меньшая из них равна x. На рисунке эта дуга обозначена AB. Тогда остальные дуги — BC и AC — можно выразить через AB: дуга BC = 3x; AC = 5x. В сумме эти дуги дают 360 градусов:
AB + BC + AC = 360;
x + 3x + 5x = 360;
9x = 360;
x = 40.
Теперь рассмотрим большую дугу AC, которая не содержит точку B. Эта дуга, как и соответствующий центральный угол AOC, равна 5x = 5 · 40 = 200 градусов.
Угол ABC — самый большой из всех углов треугольника. Это вписанный угол, опирающийся на ту же дугу, что и центральный угол AOC. Значит, угол ABC в 2 раза меньше AOC. Имеем:
ABC = AOC : 2 = 200 : 2 = 100
Это и будет градусная мера большего угла в треугольнике ABC.
Эту теорему многие забывают. А зря, ведь некоторые задачи B8 без нее вообще не решаются. Точнее, решаются, но с таким объемом вычислений, что вы скорее уснете, чем дойдете до ответа.
Теорема. Центр окружности, описанной вокруг прямоугольного треугольника, лежит на середине гипотенузы.
Что следует из этой теоремы?
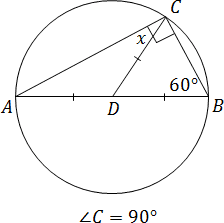
В треугольнике ABC провели медиану CD. Угол C равен 90°, а угол B — 60°. Найдите угол ACD.
Поскольку угол C равен 90°, треугольник ABC — прямоугольный. Получается, что CD — медиана, проведенная к гипотенузе. Значит, треугольники ADC и BDC — равнобедренные.
В частности, рассмотрим треугольник ADC. В нем AD = CD. Но в равнобедренном треугольнике углы при основании равны — см. «Задача B8: отрезки и углы в треугольниках». Поэтому искомый угол ACD = A.
Итак, осталось выяснить, чему равен угол A. Для этого снова обратимся к исходному треугольнику ABC. Обозначим угол A = x. Поскольку сумма углов в любом треугольнике равна 180°, имеем:
A + B + BCA = 180;
x + 60 + 90 = 180;
x = 30.
Разумеется, последнюю задачу можно решить по-другому. Например, легко доказать, что треугольник BCD — не просто равнобедренный, а равносторонний. Значит, угол BCD равен 60 градусов. Отсюда угол ACD равен 90 − 60 = 30 градусов. Как видите, можно использовать разные равнобедренные треугольники, но ответ всегда будет один и тот же.