Это классическая задача из реальной жизни: терминал берет огромную комиссию, а нам надо рассчитать, сколько денег в итоге попадет на счет.
Этот видеоурок — последний из серии уроков, посвященных задачам B1 на проценты из ЕГЭ по математике. Все последние уроки мы разбирали нестандартные задачи на проценты, и сегодняшнее видео не будет исключением, поэтому мы разберем задачу, на которой «погорело» очень много учеников, особенно в пробниках. Итак, задача:
Задача B1. При оплате через платежный терминал взимается комиссия 45%. Терминал принимает суммы, кратные 10 рублям. Месячная плата за интернет составляет 350 рублей. Какую минимальную сумму нужно заплатить через терминал, чтобы на счету фирмы, предоставляющей интернет-услуги, оказалась сумма, не меньшая 350 рублей?
Что ж, давайте решать. В первую очередь, предлагаю вспомнить формулу простых процентов, потому что в задачах про комиссии, налоги и скидки формула простых процентов работает великолепно.
Теорема о простых процентах. Пусть x — исходное значение некоторой величины (в нашем случае — это сумма, положенная в терминал), k — проценты, на которые данная величина изменяется (в нашем случае очевидно, что k — это 45%), и, наконец, y — это величина, полученная из исходной после изменения на k процентов. Тогда все три величины связаны следующей формулой:
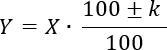
Плюс или минус перед коэффициентом k ставится в зависимости оттого, увеличивается или уменьшается исходная величина. В нашем случае, поскольку речь идет про комиссию, очевидно, что исходная величина подвергается уменьшению, то есть на счет интернет-провайдера будет зачислена меньшая сумма, чем была положена через терминал.
Но есть и еще одна проблема: мы не знаем то самое исходное значение x, нам его требуется найти в условии задачи. Однако мы знаем y. По условию нам нужно, чтобы итоговое значение величины было не менее 350 рублей. Давайте подставим все числа в формулу. Получаем:
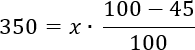
Сосчитаем, чему равен числитель и получим:
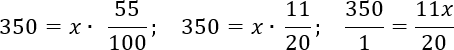
В процессе решения мы разделили числитель и знаменатель правой дроби на 5, а затем внесли переменную x в числитель правой дроби. При этом число 350 представили как 350/1, чтобы получить пропорцию.
Воспользуемся основным свойством пропорции: произведение крайних членов равно произведению средних членов. В нашем случае это выглядит так:
350 · 20 = 11x;
11x = 7000
Это простейшее линейное уравнение, и для того, чтобы найти x, нужно обе его стороны разделить на 11. Получаем:
x = 7000/11
В этой дроби ничто ни на что не сокращается, поэтому переводить в десятичную дробь придется уголком:
![]()
По условию от нас требуется найти минимальную сумму, которую нужно заплатить через терминал. Поэтому округляем наше число в большую сторону. Получаем 637. Но это еще не ответ! Дело в том, что по условию задачи терминал принимает суммы, кратные 10 рублям. Поэтому полученную сумму нужно еще раз округлить, но уже с точностью до десятков, т.е. получим 640. Разумеется, мы опять же округляем в большую сторону.
Другими словами, чтобы накопить в терминале 637 рублей десятирублевыми купюрами, потребуется положить минимум 640 рублей. Это и есть ответ к задаче — 640 рублей.
Как видите, итоговая сумма оказалась намного больше, чем 350 рублей, которые необходимо положить на счет. И это вполне логично, учитывая «грабительскую» комиссию терминала. Главный вывод отсюда следующий: учитесь обходиться без уличных терминалов оплаты, используйте кредитные карты, интернет-банки или вносите деньги непосредственно в кассу оператора. В крайнем случае, ищите терминалы, принимающие оплату без комиссии, потому что хватит кормить уличных барыг. Тратить 640 рублей, чтобы получить на счет 350 — это уже перебор.
Надеюсь, данный урок был полезен вам как с практической, так и с теоретической точки зрения. А у меня на этом все, с вами был Павел Бердов, до новых встреч!