Совершенно необязательно, что в задаче C5 попадутся корни, симметричные относительно начала координат. Потому что в противном случае все варианты ЕГЭ по математике оказались бы похожими друг на друга.
Очень часто авторы задач специально добавляют сдвиг графиков вдоль оси абсцисс. Это может запутать неподготовленного ученика — он просто не увидит, где в исходном уравнении скрыты симметричные корни.
Но мы-то с вами знаем, что такие корни есть.:) И сегодня научимся выделять их независимо от внешнего вида задачи.
Когда вы решаете квадратное уравнение относительно синуса или косинуса, то в ответе получается много отдельных множеств, работать с которыми крайне неудобно. Поэтому сегодня мы научимся объединять их, научимся искать симметрию в наборах корней и упрощать себе ответы, а, следовательно, и работу с множествами.
На самом деле существует два способа упростить решение квадратных тождеств при помощи метода симметрии. Назовем их условно геометрическим и алгебраическим. Алгебраический подход рассказывается в школе, но большинство учеников пропускают этот метод мимо ушей. Поэтому сегодняшний видео урок будет состоять из двух частей: первой — целиком посвященной геометрическому подходу, когда мы отмечаем корни на тригонометрическом круге и ищем симметрию, а второй части — в ней рассказывается о формулах понижения степеней для установления симметрии. Итак, начнем.
\[{{\cos }^{2}}=\frac{3}{4}\]
Сначала избавляемся от квадрата. Как всегда, если функция в квадрате равна какому-либо числу, то сама функция равна либо корню из этого числа, либо «минус» корню из этого числа:
\[{{f}^{2}}=a\]
\[\left[ \begin{align}& f=\sqrt{a} \\& f=-\sqrt{a} \\\end{align} \right.\]
\[a\ge 0\]
Решаем уравнение, чтобы найти корни выражения:
\[\cos x=\sqrt{\frac{3}{4}}\]
\[\cos x=\frac{\sqrt{3}}{2}\]
\[x=\pm \frac{\text{ }\!\!\pi\!\!\text{ }}{6}+2\pi n\]
В контексте нашего сегодняшнего урока все числа принадлежат множеству целых чисел.
\[\cos x=-\sqrt{\frac{3}{4}}\]
\[\cos x=-\frac{\sqrt{3}}{2}\]
\[x=\pm \arccos \left( -\frac{\sqrt{3}}{2} \right)+2\text{ }\!\!\pi\!\!\text{ }k\]
\[x=\pm \left( \text{ }\!\!\pi\!\!\text{ }-\frac{\pi }{6} \right)+2\text{ }\!\!\pi\!\!\text{ }k\]
\[x=\pm \frac{5\text{ }\!\!\pi\!\!\text{ }}{6}+2\text{ }\!\!\pi\!\!\text{ }k\]
Вот мы и получили два множества. Давайте отметим эти числа на тригонометрической окружности и найдем корни:
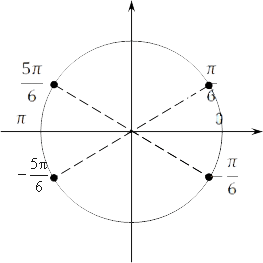
Наше множество сводится к четырем точкам. А теперь заметим, что $\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$ и $-\frac{5\text{ }\!\!\pi\!\!\text{ }}{6}$ симметричны относительно начала координат. В их симметрии легко убедиться, если вычесть из одного числа другое. Например:
\[\frac{\text{ }\!\!\pi\!\!\text{ }}{6}-\left( -\frac{5\text{ }\!\!\pi\!\!\text{ }}{6} \right)=\text{ }\!\!\pi\!\!\text{ }\]
Другими словами, расстояние между ними по окружности равно $\text{ }\!\!\pi\!\!\text{ }$.
То же самое можно сказать про $-\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$ и $\frac{5\text{ }\!\!\pi\!\!\text{ }}{6}$ — они симметричны друг другу относительно начала координат или, другими словами, можно сказать, что они лежат на одном диаметре. Если идти по нашей окружности, то расстояние между ними будет равно $\text{ }\!\!\pi\!\!\text{ }$, а это значит, что если мы возьмем точку $\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$, а потом шагнем от нее на $\text{ }\!\!\pi\!\!\text{ }$, то получим $-\frac{5\text{ }\!\!\pi\!\!\text{ }}{6}$. Потом еще шагнем на $\text{ }\!\!\pi\!\!\text{ }$ — снова попадем в $\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$, но уже $+2\text{ }\!\!\pi\!\!\text{ }$. И так постоянно прибавляя $\text{ }\!\!\pi\!\!\text{ }$, мы охватим все точки вида $\frac{\text{ }\!\!\pi\!\!\text{ }}{6}+2\text{ }\!\!\pi\!\!\text{ }$ и $-\frac{\text{ }\!\!\pi\!\!\text{ }}{6}+2\text{ }\!\!\pi\!\!\text{ k}$. Таким образом, мы можем записать эти корни уравнения в виде одного множества:
\[\frac{\text{ }\!\!\pi\!\!\text{ }}{6}+\pi k\]
Теперь разберемся со вторым набором. Тут все то же самое:\[-\frac{\text{ }\!\!\pi\!\!\text{ }}{6}+\text{ }\!\!\pi\!\!\text{ }k\]. Таким образом, мы можем просто спереди поставить ±, и это будет наш окончательный ответ:
\[x=\pm \frac{\text{ }\!\!\pi\!\!\text{ }}{6}+\text{ }\!\!\pi\!\!\text{ }k\]
Вместо четырех множеств (или двух) мы получили одно. В этом и состоит смысл симметрии корней. В дальнейшем, когда нам нужно будет что-то сделать с этими корнями, мы уже будем работать не с 4 наборами, а всего лишь с двумя.
\[{{\sin }^{2}}x=1\]
Опять же используем наши выкладки и избавляемся от квадрата:
\[\sin x=1\]
\[x=\frac{\text{ }\!\!\pi\!\!\text{ }}{2}+2\text{ }\!\!\pi\!\!\text{ }n\]
И второе выражение:
\[\begin{array}{·{35}{l}}
\sin x=-1 \\x=-\frac{\text{ }\!\!\pi\!\!\text{ }}{2}\text{+}2\text{ }\!\!\pi\!\!\text{ }k \\\end{array}\]
Отмечаем эти числа на окружности:
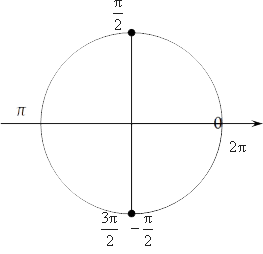
Из рисунка становится очевидно, что эти точки лежат на одном диаметре — он является осью $Oy$, осью синусов. Это значит, чтобы получить из\[\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}+2\text{ }\!\!\pi\!\!\text{ }n\]\[-\frac{\text{ }\!\!\pi\!\!\text{ }}{2}+2\text{ }\!\!\pi\!\!\text{ }k\], достаточно шагнуть из $\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}$ до $-\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}$ на $\text{ }\!\!\pi\!\!\text{ }$. Таким образом мы объединяем два множества корней и получаем:
\[x=\frac{\text{ }\!\!\pi\!\!\text{ }}{2}+\text{ }\!\!\pi\!\!\text{ }n\]
\[{{\sin }^{2}}x=\frac{1}{2}\]
Снова считаем по нашим выкладкам:
\[\sin x=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}\]
\[\sin x=\frac{\sqrt{2}}{2}\]
\[x=\frac{\text{ }\!\!\pi\!\!\text{ }}{4}+2\text{ }\!\!\pi\!\!\text{ }n\]
\[x=\text{ }\!\!\pi\!\!\text{ }-\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}+2\text{ }\!\!\pi\!\!\text{ }n\]
\[x=\frac{3\text{ }\!\!\pi\!\!\text{ }}{4}+2\text{ }\!\!\pi\!\!\text{ }n\]
Переходим ко второму выражению:
\[\sin x=-\frac{\sqrt{2}}{2}\]
\[x=-\frac{\text{ }\!\!\pi\!\!\text{ }}{4}+2\text{ }\!\!\pi\!\!\text{ }l\]
\[x=\text{ }\!\!\pi\!\!\text{ }-\left( -\frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)+2\text{ }\!\!\pi\!\!\text{ }m\]
\[x=\text{ }\!\!\pi\!\!\text{ }+\frac{\text{ }\!\!\pi\!\!\text{ }}{4}+2\text{ }\!\!\pi\!\!\text{ }m\]
\[x=\frac{5\text{ }\!\!\pi\!\!\text{ }}{4}+2\text{ }\!\!\pi\!\!\text{ }m\]
Вот мы и получили четыре набора корней. Давайте отметим их:
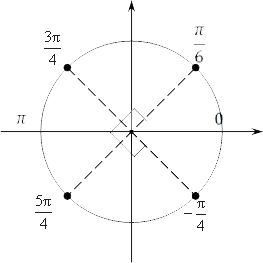
Еще очень важно, что между $\frac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}$ и $\frac{\text{ }\!\!\pi\!\!\text{ }}{4}$ угол равен 90°. Также и между $\frac{5\text{ }\!\!\pi\!\!\text{ }}{4}$ и $-\frac{\text{ }\!\!\pi\!\!\text{ }}{4}$ угол равен 90°. Наконец, и между $\frac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}$и $\frac{5\text{ }\!\!\pi\!\!\text{ }}{4}$ угол тоже равен 90°. Это значит, что все четыре точки мы можем свести к одной точке вида\[\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}+\frac{\text{ }\!\!\pi\!\!\text{ }n}{2}\].
На первый взгляд эта конструкция, все эти вычисления могут показаться очень сложными. Геометрический подход, действительно, понимают не все ученики. Однако стоит немного потренироваться, и вы будете щелкать квадратные равенства как орешки и находить симметрию между корнями.
Итак, вторая часть урока об оптимизации и объединении корней квадратных тригонометрических уравнений. Выше мы обсуждали геометрический подход, когда отмечали все корни окружности и искали какие-либо закономерности при помощи метода симметрии. В этот раз будем использовать только алгебраический подход. Все, что нам потребуется для решения — это формула косинуса двойного угла:
\[\cos 2x=2{{\cos }^{2}}x-1\]
Давайте немного преобразуем ее:
\[\cos 2x+1=2{{\cos }^{2}}x\]
\[{{\cos }^{2}}x=\frac{\cos 2x+1}{2}\]
\[{{\cos }^{2}}x=\frac{1+\cos 2x}{2}\]
Но как мы знаем, эти выкладки можно переписать и по-другому, а именно:
\[\cos 2x=1-2{{\sin }^{2}}x\]
Давайте выразим отсюда $2{{\sin }^{2}}x$:
\[2{{\sin }^{2}}x=1-\cos 2x\]
\[{{\sin }^{2}}x=\frac{1-\cos 2x}{2}\]
Вот эти две конструкции сейчас мы и будем использовать, чтобы установить симметрию между корнями.
\[{{\cos }^{2}}x=\frac{3}{4}\]
Заменяем ${{\cos }^{2}}x$:
\[\frac{1+\cos 2x}{2}=\frac{3}{4}\]
Воспользуемся основным свойством пропорции:
\[\left( 1+\cos 2x \right)\cdot 4=6\]
\[4+4\cos 2x=6\]
\[4\cos 2x=2\]
\[\cos 2x=\frac{1}{2}\]
Решаемобычноетригонометрическоетождество:
\[2=\pm \frac{\text{ }\!\!\pi\!\!\text{ }}{3}+2\text{ }\!\!\pi\!\!\text{ }n,n\in Z\]
Это обычная формула, с помощью которой решаются подобные конструкции. Но у нас известно $2x$, а не $x$, поэтому разделим обе стороны на 2:
\[2=\pm \frac{\text{ }\!\!\pi\!\!\text{ }}{6}+\text{ }\!\!\pi\!\!\text{ }n,n\in Z\]
\[{{\sin }^{2}}x=1\]
Применяем нашу вторую конструкцию:
\[\frac{1-\cos 2x}{2}=\frac{1}{1}\]
Снова получили пропорцию, перемножаем крест-накрест:
\[1-\cos 2x=2\]
\[-\cos 2x=1\]
\[\cos 2x=1\]
\[2=\text{ }\!\!\pi\!\!\text{ }+2\text{ }\!\!\pi\!\!\text{ }n,n\in Z\]
\[=\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}+\text{ }\!\!\pi\!\!\text{ }n,n\in Z\]
\[{{\sin }^{2}}x=\frac{1}{2}\]
Снова применяем наши выкладки:
\[\frac{1-\cos 2x}{2}=\frac{1}{2}\]
\[1-\cos 2x=1\]
\[-\cos 2x=0\]
\[\cos 2x=0\]
\[2=\frac{\text{ }\!\!\pi\!\!\text{ }}{2}+\text{ }\!\!\pi\!\!\text{ }n,n\in Z\]
\[=\frac{\text{ }\!\!\pi\!\!\text{ }}{4}+\frac{\text{ }\!\!\pi\!\!\text{ }n}{2},n\in Z\]
Если вы сравните эти ответы с тем, что мы получили в предыдущей части этого урока, то обнаружите, что ответы абсолютно одинаковые. Мы получили один и тот же результат, используя разные подходы — геометрический с помощью тригонометрического круга и алгебраический с помощью формул понижения степеней.
Кстати, почему их так называют? Смотрите, был ${{\cos }^{2}}x$, а стал просто $\cos 2x$. То же самое и здесь: был ${{\sin }^{2}}x$, а стал просто $\sin 2x$, опять же без квадрата. Эти выкладки сокращают объем вычислений, но чтобы воспользоваться ними, их нужно знать. Кроме того, на последнем шаге везде выполняется деление на 2. Здесь тоже очень часто допускают ошибку. Нужно делить оба слагаемых на два. Каждое из слагаемых нужно разделить на два, и тогда уравнение относительно синуса и косинуса становится элементарным.
Решая уравнения, квадратные относительно синуса или косинуса, вы постоянно будете натыкаться на громоздкие ответы, работать с которыми (например, для отбора корней) совершенно невозможно. Однако при желании можно значительно упростить эти конструкции. И сегодня мы поговорим о двух методах упрощения:
Вы можете использовать любой прием — ответ получится один и тот же. Кому-то (например, мне) удобнее отмечать точки на тригонометрическом круге, а кому-то проще раз и навсегда запомнить выкладки понижения степени (которые, кстати, совсем несложные).
Тут все банально. Решаем равенство, отмечаем полученные корни на круге, а затем ищем какую-нибудь закономерность в их расположении. Например, корни могут отстоять друг от друга на половину исходного периода, либо располагаться симметрично относительно начала координат.
Это уникальная фишка, которая работает только в тригонометрических уравнениях. Уравнения, квадратные относительно синуса или косинуса, легко сводятся к равносильным линейным. Для этого потребуется только знать формулы косинуса двойного угла:
\[\cos 2x=2\cos 2\text{ }x-1;\]
\[\cos 2x=1-2\sin 2x.\]