Сегодня мы изучим еще более сложную задачу на поиск точек экстремума из ЕГЭ по математике. Взгляните:
Найдите произведение всех точек максимума функции:
\[y={{x}^{4}}{{e}^{-{{x}^{2}}}}\]
Сразу хочу обратить ваше внимание: в степени стоит именно $-{{x}^{2}}$, не линейная функция, а именно квадратичная. И, следовательно, для решения этой задачи нам придется привлекать производную сложной функции. Но прежде чем мы начнем решать эту задачу, хотелось бы вспомнить общий алгоритм. Напомню, что для нахождения экстремума нам потребуется выполнить четыре последовательных шага:
Хватит теории, давайте решим нашу задачу. В первую очередь заметим, что перед нами произведение двух функций, следовательно, для решения задачи потребуется вспомнить формулу производной произведения, а именно:
\[{{\left( f\cdot g \right)}^{\prime }}={f}'\cdot g+f\cdot {g}'\]
Давайте воспользуемся этой формулой для нахождения производной сложной функции:
\[{y}'={{\left( {{x}^{4}}\cdot {{e}^{-{{x}^{2}}}} \right)}^{\prime }}={{\left( {{x}^{4}} \right)}^{\prime }}\cdot {{e}^{-{{x}^{2}}}}+{{x}^{4}}...\]
При вычислении у нас может возникнуть заминка, поэтому давайте выпишем сложную функцию отдельно. Перед нами производная сложной функции, следовательно, чтобы найти ее, необходимо ввести новую переменную:
\[-{{x}^{2}}=t\]
Получим:
\[{{\left( {{e}^{-{{x}^{2}}}} \right)}^{\prime }}={{\left( {{e}^{t}} \right)}^{\prime }}\cdot {t}'\]
Это и есть формула производной сложной функции. Другими словами, если мы вводим новую переменную, то в дальнейшем мы обязаны умножить на производную этой переменной, чтобы получить производную исходной функции. Давайтепосчитаем:
\[{{\left( {{e}^{-{{x}^{2}}}} \right)}^{\prime }}={{\left( {{e}^{t}} \right)}^{\prime }}\cdot {t}'={{e}^{-{{x}^{2}}}}\cdot {{\left( -{{x}^{2}} \right)}^{\prime }}={{e}^{-{{x}^{2}}}}\cdot \text{ }\left( -2x \right)\]
Производная сложной функции найдена. Возвращаемся к нашей исходной функции и дописываем:
\[{y}'={{\left( {{x}^{4}}\cdot {{e}^{-{{x}^{2}}}} \right)}^{\prime }}={{\left( {{x}^{4}} \right)}^{\prime }}\cdot {{e}^{-{{x}^{2}}}}+{{x}^{4}}\cdot {{e}^{-{{x}^{2}}}}\cdot \left( -2x \right)=\]
\[={{x}^{3}}\cdot {{e}^{-{{x}^{2}}}}\left( 4\cdot 1\cdot 1+x\cdot 1\cdot \left( -2x \right) \right)={{x}^{3}}\cdot {{e}^{-{{x}^{2}}}}\left( 4-2{{x}^{2}} \right)=\]
\[=2{{x}^{3}}\cdot {{e}^{-{{x}^{2}}}}\left( 2-{{x}^{2}} \right)\]
Переходим ко второму шагу и приравниваем ее к нулю. Решаем полученное уравнение:
\[2{{x}^{3}}\cdot {{e}^{-{{x}^{2}}}}\left( 2-{{x}^{2}} \right)=0\]
Произведение равно 0, когда хотя бы один из множителей равен 0. Очевидно, что 2 никогда не равна 0, поэтому остаются следующие варианты:
\[\left[ \begin{align}& {{x}^{3}}=0, \\& {{e}^{-{{x}^{2}}}}=0, \\& 2-{{x}^{2}}=0. \\\end{align} \right.=>\left[ \begin{align}& x=0, \\& \varnothing , \\& {{x}^{2}}=2. \\\end{align} \right.=>\left[ \begin{align}& x=0, \\& x=\sqrt{2}, \\& x=-\sqrt{2}. \\\end{align} \right.\]
Итого у нас три корня, причем первый из них имеет третью кратность.
Переходим к третьему шагу и отмечаем все три значения на координатной оси:
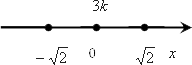
Осталось разобраться со знаками. Давайте возьмем какое-нибудь большое число, например, 1000, и подставим наше число в ${y}'$:
\[2{{x}^{3}}\cdot {{e}^{-{{x}^{2}}}}\left( 2-{{x}^{2}} \right)\]
итоге первое число будет отрицательным, т. е. будет стоять «минус». Затем,\[\sqrt{2}\]является корнем первой кратности, следовательно, при переходе через него знак поменяется. Знак также поменяется при переходе через 0, потому что 0 является корнем третьей кратности, а 3 — это число нечетное. Напоминаю, что при переходе через корень нечетной кратности знак меняется, а при переходе через корень четной кратности — 2, 8 и т. д. знак остается прежним. В нашем случае все меняется. И при переходе через корень\[-\sqrt{2}\]знак также меняется:
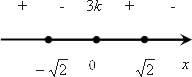
Прекрасно, мы отметили все корни, переходим с условию задачи: от нас требуется найти произведение всех точек максимума, т. е. такие значения, которые согласно нашему четвертому шагу стоят на границе между «плюсом» и «минусом». Таких у нас будет две:\[\sqrt{2}\]и\[-\sqrt{2}\].
А теперь возвращаемся к условию задачи и смотрим: от нас требуется найти их произведение. Запишем:
\[-\sqrt{2}\text{ }\!\!\cdot\!\!\text{ }\sqrt{\text{2}}=-2\]
Ответ к задаче будет -2.
Основная проблема, с которой столкнется большинство учеников — это производная сложной функции. К сожалению, в школе недостаточно уделяют внимание как производным вообще, так и сложным производным в частности. В результате многие ученики не то, что производную сложной функции не могут вспомнить, они даже не подозревают о существовании формулы производной произведения. Очень часто я наблюдаю такую ситуацию: человек хочет сосчитать производную произведения, и считает ее следующим образом:
\[{{\left( {{x}^{4}} \right)}^{\prime }}\cdot {{\left( {{e}^{-{{x}^{2}}}} \right)}^{\prime }}\]
Другими словами, многие ученики искренне считают, что производная произведения равна произведению производных. Это неправильно, ни в коем случае нельзя так считать, а правильно считать нужно с помощью специальной формулы:
\[{{\left( f\cdot g \right)}^{\prime }}={f}'\cdot g+f\cdot {g}'\]
Надеюсь, этот урок поможет тем, кто готовится к ЕГЭ по математике. Смотрите другие видеоуроки, решайте задачи — и никакие экзамены вам будут не страшны!