Все задачи B7, которые мне доводилось видеть, были сформулированы примерно одинаково: решить уравнение. При этом сами уравнения относятся к одному из трех видов:
Вообще говоря, полноценное руководство по каждому типу уравнений займет не один десяток страниц, выходя далеко за рамки ЕГЭ. Поэтому мы рассмотрим лишь самые простые случаи, требующие незатейливых рассуждений и выкладок. Этих знаний будет вполне достаточно, чтобы решить любую задачу B7.
В математике термин «решить уравнение» означает найти множество всех корней данного уравнения, либо доказать, что это множество пусто. Но в бланк ЕГЭ можно вписывать только числа — никаких множеств. Поэтому, если в задании B7 оказалось больше одного корня (или, наоборот, ни одного) — в решении была допущена ошибка.
Логарифмическое уравнение — это любое уравнение, которое сводится к виду log a f(x) = k, где a > 0, a ≠ 1 — основание логарифма, f(x) — произвольная функция, k — некоторая постоянная.
Такое уравнение решается внесением постоянной k под знак логарифма: k = log a a k . Основание нового логарифма равно основанию исходного. Получим уравнение log a f(x) = log a a k , которое решается отбрасыванием логарифма.
Заметим, что по условию a > 0, поэтому f(x) = a k > 0, т.е. исходный логарифм существует.
Задача. Решить уравнение: log7 (8 − x) = 2.
Решение. log7 (8 − x) = 2 ⇔ log7 (8 − x) = log7 72 ⇔ 8 − x = 49 ⇔ x = −41.
Задача. Решить уравнение: log0,5 (6 − x) = −2.
Решение. log0,5 (6 − x) = −2 ⇔ log0,5 (6 − x) = log0,5 0,5−2 ⇔ 6 − x = 4 ⇔ x = 2.
Но что делать, если исходное уравнение окажется сложнее, чем стандартное log a f(x) = k? Тогда сводим его к стандартному, собирая все логарифмы в одной стороне, а числа — в другой.
Если в исходном уравнении присутствует более одного логарифма, придется искать область допустимых значений (ОДЗ) каждой функции, стоящей под логарифмом. Иначе могут появиться лишние корни.
Задача. Решить уравнение: log5 (x + 1) + log5 (x + 5) = 1.
Поскольку в уравнении присутствуют два логарифма, найдем ОДЗ:
Получаем, что ОДЗ — это интервал (−1, +∞). Теперь решаем уравнение:
log5 (x + 1) + log5 (x + 5) = 1 ⇒ log5 (x + 1)(x + 5) = 1 ⇔ log5 (x + 1)(x + 5) = log5 51 ⇔ (x + 1)(x + 5) = 5 ⇔ x 2 + 6x + 5 = 5 ⇔ x (x + 6) = 0 ⇔ x 1 = 0, x 2 = −6.
Но x 2 = −6 не подходит по ОДЗ. Остается корень x 1 = 0.
Показательное уравнение — это любое уравнение, которое сводится к виду a f(x) = k, где a > 0, a ≠ 1 — основание степени, f(x) — произвольная функция, k — некоторая постоянная.
Это определение почти дословно повторяет определение логарифмического уравнения. Решаются показательные уравнения даже проще, чем логарифмические, ведь здесь не требуется, чтобы функция f(x) была положительна.
Для решения сделаем замену k = a t , где t — вообще говоря, логарифм (t = log a k), но в ЕГЭ числа a и k будут подобраны так, что найти t будет легко. В полученном уравнении a f(x) = a t основания равны, а значит, равны и показатели, т.е. f(x) = t. Решение последнего уравнения, как правило, не вызывает проблем.
Задача. Решить уравнение: 7 x − 2 = 49.
Решение. 7 x − 2 = 49 ⇔ 7 x − 2 = 72 ⇔ x − 2 = 2 ⇔ x = 4.
Задача. Решить уравнение: 616 − x = 1/36.
Решение. 616 − x = 1/36 ⇔ 616 − x = 6−2 ⇔ 16 − x = −2 ⇔ x = 18.
Немного о преобразовании показательных уравнений. Если исходное уравнение отличается от a f(x) = k, применяем правила работы со степенями:
Кроме того, надо знать правила замены корней и дробей на степени с рациональным показателем:
Такие уравнения встречаются в ЕГЭ крайне редко, но без них разбор задачи B7 был бы неполным.
Задача. Решить уравнение: (5/7) x − 2 · (7/5)2x − 1 = 125/343
Заметим, что:
Имеем: (5/7) x − 2 · (7/5)2x − 1 = 125/343 ⇔ (5/7) x − 2 · (5/7)1 − 2x = (5/7)3 ⇔ (5/7) x − 2 + 1 − 2x = (5/7)3 ⇔ (5/7)−x − 1 = (5/7)3 ⇔ −x − 1 = 3 ⇔ x = −4.
Под иррациональным понимается любое уравнение, содержащее знак корня. Из всего многообразия иррациональных уравнений мы рассмотрим лишь простейший случай, когда уравнение имеет вид:
Чтобы решить такое уравнение, возведем обе стороны в квадрат. Получим уравнение f(x) = a 2. При этом автоматически выполняется требование ОДЗ: f(x) ≥ 0, т.к. a 2 ≥ 0. Остается решить несложное уравнение f(x) = a 2.
Задача. Решить уравнение:
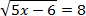
Возводим обе стороны в квадрат и получим: 5x − 6 = 82 ⇔ 5x − 6 = 64 ⇔ 5x = 70 ⇔ x = 14.
Задача. Решить уравнение:
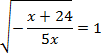
Сначала, как и в прошлый раз, возводим обе стороны в квадрат. А затем внесем знак «минус» в числитель. Имеем:
Заметим, что при x = −4 под корнем будет положительное число, т.е. требование ОДЗ выполнено.