На уроках алгебры учителя рассказывают, что существует небольшой (на самом деле — очень даже большой) класс тригонометрических уравнений, которые не решаются стандартными способами — ни через разложение на множители, ни через замену переменной, ни даже через однородные слагаемые. В этом случае в дело вступает принципиально другой подход — метод вспомогательного угла.
Что это за метод и как его применять? Для начала вспомним формулы синуса суммы/разности и косинуса суммы/разности:
\[\begin{align}& \sin \left( \alpha \pm \beta \right)=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta \\& \cos \left( \alpha \pm \beta \right)=\cos \alpha \cos \beta \mp \sin \alpha \sin \beta \\\end{align}\]
Думаю, эти формулы хорошо знакомы вам — из них выводятся формулы двойного аргумента, без которых в тригонометрии вообще никуда. Но давайте теперь рассмотрим простое уравнение:
\[3\sin x+4\cos x=5\]
Разделим обе части на 5:
\[\frac{3}{5}\sin x+\frac{4}{5}\cos x=1\]
Заметим, что ${{\left( \frac{3}{5} \right)}^{2}}+{{\left( \frac{4}{5} \right)}^{2}}=1$, а это значит, что обязательно найдётся такой угол $\alpha $, для которого эти числа являются соответственно косинусом и синусом. Поэтому наше уравнение перепишется следующим образом:
\[\begin{align}& \cos \alpha \sin x+\sin \alpha \cos x=1 \\& \sin \left( \alpha +x \right)=1 \\\end{align}\]
А это уже легко решается, после чего останется лишь выяснить, чему равен угол $\alpha $. Как это выяснить, а также как правильно подбирать число для деления обеих частей уравнения (в данном простом примере мы делили на 5) — об этом в сегодняшнем видеоуроке:
Сегодня мы будем разбирать решение тригонометрических уравнений, а, точнее, один-единственный прием, который называется «метод вспомогательного угла». Почему именно этот метод? Просто потому, что за последние два-три дня, когда я занимался с учениками, которым рассказывал о решении тригонометрических уравнений, и мы разбирали, в том числе, метод вспомогательного угла, и все ученики как один допускают одну и ту же ошибку. А ведь метод вообщем-то несложный и, более того, это один из основных приемов в тригонометрии. Поэтому многие тригонометрические задачи иначе как методом вспомогательного угла вообще не решаются.
Поэтому сейчас для начала мы рассмотрим пару простеньких задач, а потом перейдем к задачам посерьезней. Однако все эти они так или иначе потребуют от нас применение метода вспомогательного угла, суть которого я расскажу уже в первой конструкции.
\[\cos 2x=\sqrt{3}\sin 2x-1\]
Немного преобразуем наше выражение:
\[\cos 2x-\sqrt{3}\sin 2x=-1\left| \left( -1 \right) \right.\]
\[\sqrt{3}\cdot \sin 2x-\cos 2x=1\]
Как мы будем решать его? Стандартный прием состоит в том, чтобы раскрыть $\sin 2x$ и $\cos 2x$ по формулам двойного угла, а затем переписать единицу как ${{\sin }^{2}}x{{\cos }^{2}}x$, получить однородное уравнение, привести его к тангенсам и решить. Однако это долгий и нудный путь, который требует большого объема вычислений.
Предлагаю задуматься вот на чем. У нас есть $\sin $ и $\cos $. Вспомним формулу косинуса и синуса суммы и разности:
\[\sin \left( \alpha \pm \beta \right)=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta \]
\[\cos \left( \alpha +\beta \right)=\cos \alpha \cos \beta -\sin \alpha \sin \beta \]
\[\cos \left( \alpha -\beta \right)=\cos a\cos \beta +\sin \alpha \sin \beta \]
Вернемся к нашему примеру. Все сведем к синусу разности. Но для начала уравнение необходимо немного преобразовать. Найдем коэффициент:
\[l={{\left( \sqrt{3} \right)}^{2}}+{{\left( -1 \right)}^{2}}=3+1=4\]
\[\sqrt{l}=2\]
$\sqrt{l}$ — это тот самый коэффициент, на который необходимо разделить обе части уравнения, чтобы перед синусом и косинусом появились числа, которые сами по себе являются синусами и косинусами. Давайте разделим:
\[\frac{\sqrt{3}}{2}\cdot \sin 2x-\frac{1}{2}\cdot \cos 2x=\frac{1}{2}\]
Посмотрим на то, что у нас получилось слева: существует ли такой $\sin $ и $\cos $, чтобы $\cos \alpha =\frac{\sqrt{3}}{2}$, а $\sin \alpha =\frac{1}{2}$? Очевидно существует: $\alpha =\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$. Поэтому мы можем переписать наше выражение следующим образом:
\[\cos \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\cdot \sin 2x-\sin \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\cdot \cos 2x=\frac{1}{2}\]
\[\sin 2x\cdot \cos \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}-\cos 2x\cdot \sin \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}=\frac{1}{2}\]
Теперь перед нами формула синуса разности. Мы можем написать так:
\[\sin \left( 2x-\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}} \right)=\frac{1}{2}\]
Перед нами простейшая классическая тригонометрическая конструкция. Напомню:
\[\sin x=a\]
\[x=\arcsin a+2\text{ }\!\!\pi\!\!\text{ }n\]
\[x=\text{ }\!\!\pi\!\!\text{ }-\arcsin a-2\text{ }\!\!\pi\!\!\text{ }n\]
Это и запишем для нашего конкретного выражения:
\[\left[ \begin{align}& 2x-\frac{\text{ }\!\!\pi\!\!\text{ }}{6}=\frac{\text{ }\!\!\pi\!\!\text{ }}{6}=2\text{ }\!\!\pi\!\!\text{ }n \\& 2x-\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}=\text{ }\!\!\pi\!\!\text{ }-\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}+2\text{ }\!\!\pi\!\!\text{ }n \\\end{align} \right.\]
\[\left[ \begin{align}& 2x=\frac{\text{ }\!\!\pi\!\!\text{ }}{3}+2\text{ }\!\!\pi\!\!\text{ }n \\& 2x=\text{ }\!\!\pi\!\!\text{ }+2\text{ }\!\!\pi\!\!\text{ }n \\\end{align} \right.\]
\[\]
\[\left[ \begin{align}& x=\frac{\text{ }\!\!\pi\!\!\text{ }}{6}+\text{ }\!\!\pi\!\!\text{ }n \\& x=\frac{\text{ }\!\!\pi\!\!\text{ }}{2}+\text{ }\!\!\pi\!\!\text{ }n \\\end{align} \right.\]
\[n\in Z\]
Итак, что нужно делать, если вам попалось подобный пример:
В связи с этим у внимательных учеников наверняка возникнет два вопроса.
Что нам мешает на этапе нахождения поправочного коэффициента записать $\sin $ и $\cos $? — Нам мешает основное тригонометрическое тождество. Дело в том, что полученные $\sin $ и $\cos $, как любые другие при одном и том же аргументе, должны при возведении в квадрат в сумме давать ровно «единицу». В процессе решения нужно быть очень внимательным и не потерять «двойку» перед «иксами».
Метод вспомогательного угла — это инструмент, который помогает свести «некрасивое» уравнение к вполне адекватному и «красивому».
\[\sqrt{3}\sin 2x+2{{\sin }^{2}}x-1=2\cos x\]
Мы видим, что у нас есть ${{\sin }^{2}}x$, поэтому давайте воспользуемся выкладками понижения степеней. Однако прежде чем ними воспользоваться, давайте их выведем. Для этого вспомним, как найти косинус двойного угла:
\[\cos 2x={{\cos }^{2}}x-{{\sin }^{2}}x=2{{\cos }^{2}}x-1=1-2{{\sin }^{2}}x\]
Если мы запишем $\cos 2x$ в третьем варианте, то получим:
\[\cos 2x=1-2{{\sin }^{2}}x\]
\[2{{\sin }^{2}}x=1-\cos 2x\]
\[{{\sin }^{2}}x=\frac{1-{{\cos }^{2}}x}{x}\]
Я выпишу отдельно:
\[{{\sin }^{2}}x=\frac{1-\cos 2x}{2}\]
То же самое можно сделать и для ${{\cos }^{2}}x$:
\[{{\cos }^{2}}x=\frac{1+\cos 2x}{2}\]
Нам потребуется только первые выкладки. Давайте приступим к работе над задачей:
\[\sqrt{3}\cdot \sin 2x+2\cdot \frac{1-\cos 2x}{2}-1=2\cos x\]
\[\sqrt{3}\cdot \sin 2x+1-\cos 2x-1=2\cos x\]
\[\sqrt{3}\cdot \sin 2x-\cos 2x=2\cos x\]
Теперь воспользуемся выкладками косинуса разности. Но для начала посчитаем поправку $l$:
\[l={{\left( \sqrt{3} \right)}^{2}}+{{\left( -1 \right)}^{2}}=4\]
\[\sqrt{l}=2\]
Перепишем с учетом этого факта:
\[\frac{\sqrt{3}}{2}\cdot \sin 2x-\frac{1}{2}\cdot \cos 2x=\cos x\]
В этом случае мы можем записать, что $\frac{\sqrt{3}}{2}=\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$, а $\frac{1}{2}=\cos \frac{\text{ }\!\!\pi\!\!\text{ }}{3}$. Перепишем:
\[\sin \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}\cdot \sin 2x-\cos \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}\cdot \cos 2x=\cos x\]
\[-\cos \left( \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}+2x \right)=\cos x\]
Внесем «минус» в скобку хитрым способом. Для этого заметим следующее:
\[\cos \left( \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}+2x \right)=\cos \left( \text{ }\!\!\pi\!\!\text{ }-\text{ }\!\!\pi\!\!\text{ +}\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}+2x \right)=\]
\[=\cos \left( \text{ }\!\!\pi\!\!\text{ }-\frac{2\text{ }\!\!\pi\!\!\text{ }}{3}+2x \right)=\cos \left( \text{ }\!\!\pi\!\!\text{ }+\varphi \right)=-\cos \varphi \]
Возвращаемся к нашему выражению и вспоминаем, что в роли $\varphi $ у нас выражение $-\frac{2\text{ }\!\!\pi\!\!\text{ }}{3}+2x$. Поэтому запишем:
\[-\left( -\cos \left( -\frac{2\text{ }\!\!\pi\!\!\text{ }}{3}+2x \right) \right)=\cos x\]
\[\cos \left( 2x-\frac{2\text{ }\!\!\pi\!\!\text{ }}{3} \right)=\cos x\]
Чтобы решить подобною задачу, нужно вспомнить такое:
\[\cos \alpha =\cos \beta \]
\[\left[ \begin{align}& \alpha =\beta +2\text{ }\!\!\pi\!\!\text{ }n \\& \alpha =-\beta +2\text{ }\!\!\pi\!\!\text{ }n \\\end{align} \right.\]
Разберемся с нашим примером:
\[\left[ \begin{align}& 2x-\frac{2\text{ }\!\!\pi\!\!\text{ }}{3}=x+2\text{ }\!\!\pi\!\!\text{ }n \\& 2x-\frac{2\text{ }\!\!\pi\!\!\text{ }}{3}=-x+2\text{ }\!\!\pi\!\!\text{ }n \\\end{align} \right.\]
Давайте посчитаем каждое из этих уравнений:
\[x=\frac{2\text{ }\!\!\pi\!\!\text{ }}{3}+2\text{ }\!\!\pi\!\!\text{ }n\]
И вторую:
\[3x=\frac{2\text{ }\!\!\pi\!\!\text{ }}{3}+2\text{ }\!\!\pi\!\!\text{ }\]
\[x=\frac{2\pi }{9}+\frac{2\pi n}{3}\]
Запишем окончательный ответ:
\[\left[ \begin{align}& x=\frac{2\text{ }\!\!\pi\!\!\text{ }}{3}+2\text{ }\!\!\pi\!\!\text{ }n \\& x=\frac{2\text{ }\!\!\pi\!\!\text{ }}{9}+\frac{2\text{ }\!\!\pi\!\!\text{ }n}{3} \\\end{align} \right.\]
На самом деле, это выражение решается множеством различных способов, однако именно метод вспомогательного угла является в данном случае оптимальным. Кроме того, на примере данной конструкции хотелось бы обратить ваше внимание еще на несколько интересных приемов и фактов:
Но и это еще не все. До сих пор $\sin $ и $\cos $, которые мы выводили в качестве дополнительного аргумента, мы считали, что они должны быть положительными. Поэтому сейчас мы решим более сложные задачи.
\[\sin 3x+4{{\sin }^{3}}x+4\cos x=5\]
Преобразуем первое слагаемое:
\[\sin 3x=\sin \left( 2x+x \right)=\sin 2x\cdot \cos x+\cos 2x\cdot \sin x\]
Второе:
\[4{{\sin }^{3}}x=4\cdot {{\sin }^{2}}x\cdot \sin x=4\cdot \frac{1-{{\cos }^{2}}x}{2}\cdot \sin x=\]
\[=2\left( 1-\cos 2x \right)\cdot \sin x\]
А теперь подставим все это в нашу исходную конструкцию:
\[\sin 2x\cos x+\cos 2x\sin x+2\sin x-2\cos x\sin x+4\cos x=5\]
\[\sin 2x\cos x-\operatorname{cosx}-cos2\sin x+2\sin x+4\cos x=5\]
\[\sin \left( 2x-x \right)+2\sin x+4\cos x=5\]
\[3\sin x+4\cos x=5\]
Давайте введем нашу поправку:
\[l=9+16=25\]
\[\sqrt{l}=5\]
Записываем:
\[\frac{3}{5}\sin x+\frac{4}{5}\cos x=1\]
Таких $\alpha $, для которых $\sin $ или $\cos $ был бы равен $\frac{3}{5}$ и $\frac{4}{5}$ в тригонометрической таблице нет. Поэтому давайте просто так и напишем и сведем выражение к синусу суммы:
\[\sin x\cdot \cos \varphi +\cos x\cdot \sin \varphi =1\]
\[\sin \left( x+\varphi \right)=1\]
Это частный случай, простейшая тригонометрическая конструкция:
\[x+\varphi =\frac{\text{ }\!\!\pi\!\!\text{ }}{2}+2\text{ }\!\!\pi\!\!\text{ }n\]
\[x=\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}-\varphi +2\text{ }\!\!\pi\!\!\text{ }n\]
Осталось найти, чему равен $\varphi $. Именно в этом месте многие ученики ошибаются. Дело в том, что на $\varphi $ накладываются два требования:
\[\left\{ \begin{align}& \cos \varphi =\frac{3}{5} \\& \sin \varphi =\frac{4}{5} \\\end{align} \right.\]
Начертим радар и посмотрим, где такие значения встречаются:
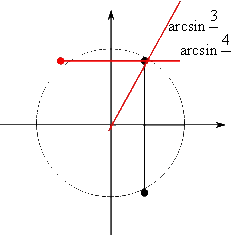
Возвращаясь к нашему выражению, мы напишем следующее:
\[x=\frac{\text{ }\!\!\pi\!\!\text{ }}{2}-\arcsin \frac{4}{5}+2\text{ }\!\!\pi\!\!\text{ }n\]
Но и эту запись можно немного оптимизировать. Поскольку мы знаем следующее:
\[\alpha :\arcsin \alpha +\arccos \alpha =\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}},\]
то в нашем случае можно записать так:
\[x=\arccos \frac{4}{5}+2\text{ }\!\!\pi\!\!\text{ }n\]
Здесь потребуется еще более глубокое понимание методик решения стандартных задач без тригонометрии. Но для решения этого примера мы также используем метод вспомогательного угла.\[\]
\[5+2\sin 2x-5\cos x=5\sin x\]
Первое, что бросается в глаза — здесь нет степеней выше первой и поэтому ничего нельзя разложить по формулам разложения степеней. Воспользуется обратными выкладками:
\[5+4\sin x\cos x-5\cos x-5\sin x=0\]
\[3+2+4\sin x\cos x-5\left( \sin x+\cos x \right)=0\]
Зачем я разложил $5$. Вот смотрите:
\[3+2\left( 1+2\sin x\cos x \right)-5\left( \sin x\cos x \right)=0\]
Единицу по основному тригонометрическому тождеству мы можем расписать как ${{\sin }^{2}}x+{{\cos }^{2}}x$:
\[3+2\left( {{\sin }^{2}}x+2\sin x\cos x+co{{s}^{2}}x \right)-5\left( \sin x+\cos x \right)=0\]
Что дает нам такая запись? Дело в том, что в первой скобке стоит точный квадрат. Свернем его и получим:
\[3+2{{\left( \sin x+\cos x \right)}^{2}}-5\left( \sin x+\cos x \right)=0\]
Предлагаю ввести новую переменную:
\[\sin x+\cos x=t\]
В этом случае мы получим выражение:
\[3+2{{t}^{2}}-5t=0\]
\[2{{t}^{2}}-5t+3=0\]
\[D=25-24=1\]
\[{{t}_{1}}=\frac{5+1}{4}=\frac{3}{2}\]
\[{{t}_{2}}=\frac{5-1}{4}=1\]
Итого мы получаем:
\[\left[ \begin{align}& \sin x+\cos x=\frac{3}{2} \\& \sin x+\cos x=1 \\\end{align} \right.\]
Разумеется, знающие ученики сейчас скажут, что такие конструкции легко решаются с помощью сведения к однородному. Однако мы решим каждое уравнение методом вспомогательного угла. Для этого сначала посчитаем поправку $l$:
\[l={{1}^{2}}+{{1}^{2}}=2\]
\[\sqrt{l}=\sqrt{2}\]
Разделим все на $\sqrt{2}$:
\[\left[ \begin{align}& \frac{\sqrt{2}}{2}\sin x+\frac{\sqrt{2}}{2}\cos x=\frac{3}{2\sqrt{2}} \\& \frac{\sqrt{2}}{2}\sin x+\frac{\sqrt{2}}{2}\cos x=\frac{\sqrt{2}}{2} \\\end{align} \right.\]
Все сведем к $\cos $:
\[\cos x\cdot \cos \frac{\text{ }\!\!\pi\!\!\text{ }}{4}+\sin x\sin \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\]
\[\left[ \begin{align}& \cos \left( x-\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}} \right)=\frac{3}{2\sqrt{2}} \\& \cos \left( x-\frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)=\frac{\sqrt{2}}{2} \\\end{align} \right.\]
Разбираемся с каждым из этих выражений.
Первое уравнение корней не имеет, и для доказательства этого факта нам поможет иррациональность в знаменателе. Заметим следующее:
\[\sqrt{2}<1,5\]
\[\frac{3}{2\sqrt{2}}>\frac{3}{3\cdot 1,5}=\frac{3}{3}=1\]
Итого мы четко доказали, что требуется, чтобы $\cos \left( x-\frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)$ был равен числу, которое большее «единицы» и, следовательно, у этой конструкции корней нет.
Разбираемся со вторым:
\[x-\frac{\text{ }\!\!\pi\!\!\text{ }}{4}=\pm \frac{\text{ }\!\!\pi\!\!\text{ }}{4}+2\text{ }\!\!\pi\!\!\text{ }n\]
Решаем эту конструкцию:
\[x=\frac{\text{ }\!\!\pi\!\!\text{ }}{4}\pm \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}+2\text{ }\!\!\pi\!\!\text{ }n\]
В принципе, можно оставить ответ таким, а можно его расписать:
\[x=\frac{\text{ }\!\!\pi\!\!\text{ }}{2}+2\text{ }\!\!\pi\!\!\text{ }n\]
\[x=2\text{ }\!\!\pi\!\!\text{ }n\]
\[n\in Z\]
В заключение хотел бы еще раз обратить ваше внимание на работу с «некрасивыми» аргументами, т.е. когда $\sin $ и $\cos $ не являются табличными значениями. Проблема состоит в том, что если мы утверждаем, что в нашем уравнении $\frac{3}{5}$ — это $\cos $, а $\frac{4}{5}$ — это $\sin $, то в итоге, после того как мы решим конструкцию, нужно учитывать оба этих требования. Мы получаем систему из двух уравнений. Если мы не будем это учитывать, то получим следующую ситуацию. В этом случае мы получим две точки и на месте $\varphi $ у нас окажется два числа: $\arcsin \frac{4}{5}$ и $-\arcsin \frac{4}{5}$, однако последний нас ни в коем случае не устраивает. То же самое будет и с точкой $\frac{3}{5}$.
Такая проблема возникает только тогда, когда речь идет о «некрасивых» аргументах. Когда у нас табличные значения, то ничего такого нет.
Надеюсь, сегодняшний урок помог вам разобраться, что такое метод вспомогательного угла и как его применять на примерах разного уровня сложности. Но это не единственный урок, посвященный решению задач методом вспомогательного угла. Поэтому оставайтесь с нами!