В этом видеоуроке мы продолжаем разбирать иррациональные неравенства вида . Благодаря прошлому уроку мы знаем, что нельзя просто взять и возвести его обе стороны в квадрат, потому что мы рискуем потерять большой кусок решения. Поэтому предлагаю еще раз записать общую формулу, по которой решаются все подобные задачи:
Erroneous nesting of equation structures
\begin{align}& \left\{ \begin{align}& g\ge 0 \\& f\rangle {{g}^{2}} \\\end{align} \right. \\& \left\{ \begin{align}& g\langle 0 \\& f\ge 0 \\\end{align} \right. \\\end{align}
Вот такая совокупность из двух выражений. Теперь с помощью этой формулы попробуем посчитать:
x+−x2+8x−12−−−−−−−−−−−√⟩4x2+8x−12−−−−−−−−−−√⟩4−x
\begin{align}& x+\sqrt{-{{x}^{2}}+8x-12}\rangle 4 \\& \sqrt{{{x}^{2}}+8x-12}\rangle 4-x \\\end{align}
Предлагаю сначала рассмотреть первую иррациональную конструкцию, когда правая часть больше или равна нулю:
{4−x≥0−x2+8x−12⟩(4−x)2
\left\{ \begin{align}& 4-x\ge 0 \\& -{{x}^{2}}+8x-12\rangle {{(4-x)}^{2}} \\\end{align} \right.
Первое решается просто:
\[\begin{array}{·{35}{l}}
4\text{ }-\text{ }\text{ }\ge \text{ }0 \\-\text{ }\ge \text{ }-4 \\\text{ }\le \text{ }4 \\\end{array}\]
Со вторым все чуть сложнее:
−x2+8x−12>16−2x2+16x−28>0|:2(−2)x2−8x+14<0
\begin{align}& -{{x}^{2}}+8x-12>16 \\& -2{{x}^{2}}+16x-28>0|:2(-2) \\& {{x}^{2}}-8x+14<0 \\\end{align}
Теперь найдем иксы:
D = 64 − 4 ⋅ 14 = 64 − 56 = 8D−−√=8√=4⋅2−−−√=22√
\begin{align}& D\text{ }=\text{ }64\text{ }-\text{ }4\text{ }\cdot \text{ }14\text{ }=\text{ }64\text{ }-\text{ }56\text{ }=\text{ }8 \\& \sqrt{D}=\sqrt{8}=\sqrt{4\cdot 2}=2\sqrt{2} \\\end{align}
Давайте найдем иксы:
x1=8+22√2=4+2√x2=4−2√
\begin{align}& {{x}_{1}}=\frac{8+2\sqrt{2}}{2}=4+\sqrt{2} \\& {{x}_{2}}=4-\sqrt{2} \\\end{align}
Мы получили два числа, отмечаем их на прямой. Поскольку неравенство строгое, точки выколотые:
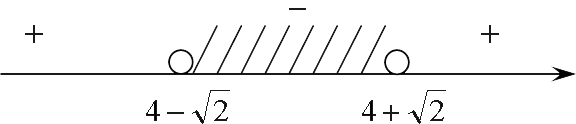
Смотрим знаки. Для этого подставим любое число, больше наших корней. Справа стоит «плюс», далее везде «плюс» и «минус» меняются, поскольку нигде нет корней четной кратности. Поскольку нам нужно найти «меньше», поэтому нас интересует интервал «минус». Осталось пересечь его решением второго неравенства. Для этого отметим наше множество на параллельных прямых:
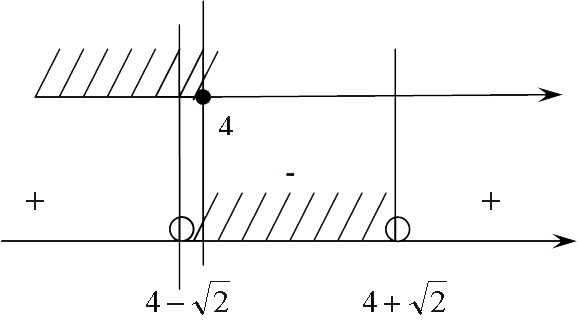
Пересекаем и видим, что единственное, что нас устраивает — это
x∈(4−2√;4]
x\in (4-\sqrt{2};4]
Переходим ко второй части нашей совокупности. Теперь мы будем требовать, чтобы правая была меньше нуля, а подкоренное выражение больше или равно нулю, т. е.:
{4−x⟨0−x2+8x−12≥0
\left\{ \begin{align}& 4-x\langle 0 \\& -{{x}^{2}}+8x-12\ge 0 \\\end{align} \right.
Вот наша вторая система. Решаем ее.
Первое неравенство иррациональной системы решается очень легко:
\[\begin{array}{·{35}{l}}
4\text{ }-\text{ }\text{ }<\text{ }0 \\-\text{ }<\text{ }-4 \\\text{ }>\text{ }4 \\\end{array}\]
Посчитаем второе:
−x2+8x−12≥0|:(−1)x2−8x+12≤0
\begin{align}& -{{x}^{2}}+8x-12\ge 0|:(-1) \\& {{x}^{2}}-8x+12\le 0 \\\end{align}
Решаем это уравнение нашей иррациональной конструкции, используя формулыВиета:
(x−6)(x−2)≤0x1=6x2=2
\begin{align}& (x-6)(x-2)\le 0 \\& {{x}^{1}}=6 \\& {{x}^{2}}=2 \\\end{align}
Отмечаем эти числа на прямой:
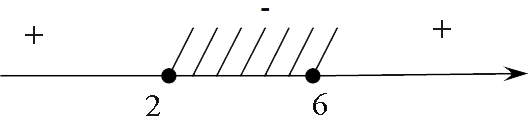
Берем 1 млрд. и подставляем в нашу конструкцию, чтобы определить знаки. Первый из них будет «плюс», далее они меняются, потому что корней четно кратности нет. Нас интересует то, что меньше 0, т. е. там, где стоит «минус».
Теперь предлагаю пересечь решение нашего неравенства с результатами второго, начертив параллельные прямые:
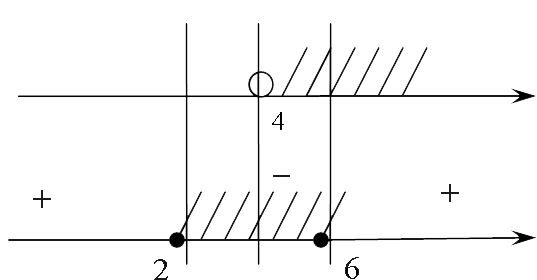
Единственный отрезок, заштрихованный на обеих прямых — это от четырех до шести до 6. Вот мы и получили ответ ко второй системе из нашей иррациональной совокупности:
∈(4; 6]
\text{ }\in \left( 4;\text{ }6 \right]
И вот мы уже очень близки к ответу. Осталось объединить интервалы, которые мы нашли. Отметим найденные точки на прямой:

От нас требуется объединить эти отрезки. Получаем:
Обратите внимание, мы именно объединили эти отрезки, а не пересекли, потому что в случае пересечения у нас бы получилось пустое множество, а не интервал.
Это ответ. Задача решена.
В предыдущем уроке (см. урок «Иррациональные неравенства. Часть 1» мы рассмотрели самый простой тип иррациональных неравенств — когда корень меньше функции. Но и там на выходе получилась система, которую надо аккуратно решать.
Сегодня мы рассмотрели более жесткий тип иррациональных неравенств, когда корень больше функции. При решении таких неравенств возникает уже две системы, решения которых надо объединить (не пересечь, а именно объединить!), чтобы получился окончательный ответ.
Поскольку на иррациональных неравенствах такого вида регулярно «обламываются» даже весьма подготовленные ученики (каюсь — сам завалил контрольную в 10-м классе), предлагаю вашему вниманию сразу два видеоурока, в которых разобран буквально каждый шаг решения. Чтобы при одном виде таких неравенств в вашей голове проскакивала мысль: «Нельзя возводить в квадрат! Тут что-то еще!»
Вот первый урок: